星煌学院チャンネル（おすすめch紹介）

チャンネル紹介

2021.12.22

【面白い数学問題】和から整数を求めよう！

(c) 星煌学院チャンネル　小学生・中学生向け学習塾を名古屋市・知多市・東海市・安城市・大府市で展開する星煌学院の動画です。 HP: https://www.sj-seico.co.jp/ …

足して28から、大きい方は、14より大きく、足して32から、小さい方は、16より小さい数であることがわかるので、2番目に大きい数が、15であることがわかる。

差が奇数である2数の和は奇数だから、和が28であることに反するということですね

先生の「はいどうも！」にお辞儀しちゃう。終わりの「バイバイ！」にバイバイしてる私。(笑)

【面白い数学問題】数列の和の求め方~応用編~

(c) 星煌学院チャンネル　前回の動画：https://youtu.be/ZNgEh2X65RU 小学生・中学生向け学習塾を名古屋市・知多市・東海市・安城市・大府市で展開する星煌 …

先頭の数字をnとして、n+(n+1)+(n+2)+・・・+(n+38)+(n+39)=2020先頭と最後尾、先頭から2つ目と後ろから2つ目、の順に足していくと、2n+39が20組できるので、20(2n+39)=202040n+780=202040n=1240n=31

中央を基点に考えるという概念はもう既に書かれてますが、40個で2020ということは一対の合計が101になる組み合わせの数字が20個というところから考察しました。101は一対なので2で割ると50.5。つまりこの前後の整数が中心になります。あとはそこから前後に19足し引きすれば31～70になりますね。

2020を40で割ったら、中央値、つまり20個目と21個目の間の数字が出ると思ったんで、そこから計算しました。

2020を20で割る　　101101になる整数の組み合わせを20組31＋70＝101 よって　31から70の整数！　　　よって31！

僕は、40個の連続するの整数の真ん中の数をnとしてn-19+n-18+n-17+…n+18+n+19+n+20=2020=40n+20よって40n=2000 n=50最小の数なのでn-19=31と出しました

初項を a とすると最後の項は a + 39 となるので、n(a_1 + a_n)/2 より、40(x + x + 39)/2 = 2020 となり、2x + 39 = 1012x = 62x = 31 と出しました。

【面白い数学問題】覆面算　Ａ～Ｆにあてはまる数字は？

どれも割切れるのですね。よく考えると7,11,13の倍数確認法(3桁ずつ区切って右から奇数番目の和から偶数番目の和を引く)で0になっているので当てはまります。

森博嗣『すべてがFになる』ですね(^-^;

16進数RGB値コードの白ですね

マッチ棒クイズ３選！

かなり考えた結果、3問目は 20-2 = 18 かなと思いました。マイナス置くにはスペースが足りないかな・・・。脳トレになって面白かったです。

別解を認めるならともかく、答えを限定させたいなら条件が不足しているといえる問題が多いですね1問目は2×2の大きさの正方形の中に1×1の正方形が重なるような解答を否定できません「同じ大きさの正方形」と指定することで解決します3問目は不等号にすることが出来ます「等式を成立させよ」とすることで解決します

最初の問題、別回答ありますね。

最初の問題大きさ違う正方形作ってもいける

3問目　202>40 じゃ駄目？

【面白い数学問題】三平方の定理を使わずに求めましょう！

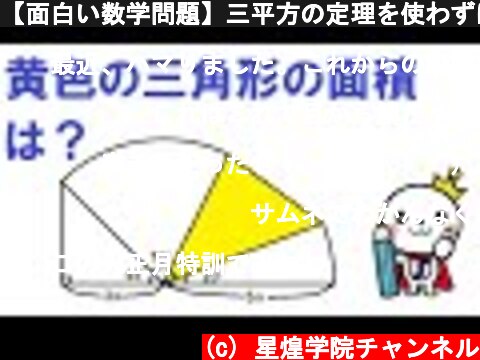
(c) 星煌学院チャンネル　（2021 愛光中）小学生・中学生向け学習塾を名古屋市・知多市・東海市・安城市・大府市で展開する星煌学院の動画です。

最近、ハマりました。これからの動画楽しみにしています

これはこれで目から鱗だったんですが、様々な解法持っていることで動画の答えがあっているか検証できるのでおすすめです。もちろん高等数学以前でも工夫で解ける趣旨かと思いますが、下記参考までに。1.(左の三角形の斜辺)=3√22.1.は求める三角形の一辺より求める三角形のうち二つの辺の長さは3√2、5で、その間の角は45°なので、求める三角形の面積は(1/2)×3√2×5×sin(45°)=(1/2)×15√2×(1/√2)=15/2すみません、結果は同じになりました！！(土下座)

楽チンだったぜ！！💪( ¨̮💪)

サムネでわかんなくてくやしーーー動画見よ！って押したら動画前の広告中にひらめけたwww

この人正月特訓でみたわ

おーい！岩下先生出してくれ！！