星煌学院チャンネル（おすすめch紹介）

チャンネル紹介

2021.12.22

【面白い数学問題】小学生でも解けて大人でも解けない図形問題４

(c) 星煌学院チャンネル　小学生・中学生向け学習塾を名古屋市・知多市・東海市・安城市・大府市で展開する星煌学院の動画です。 HP: https://www.sj-seico.co.jp/ …

皆様にお詫びがあります。元々はすべてのコメントに返信をしようと思い、時間を見つけて返信をしていました。しかし、予想以上に多くの方からコメントをいただき、コメントに返信をすることが難しくなってしまいました。コメントの返信は今後少なくなってしまいますが、できる限りコメントには目を通していきたいと思います。今後もコメントいただければ幸いです。

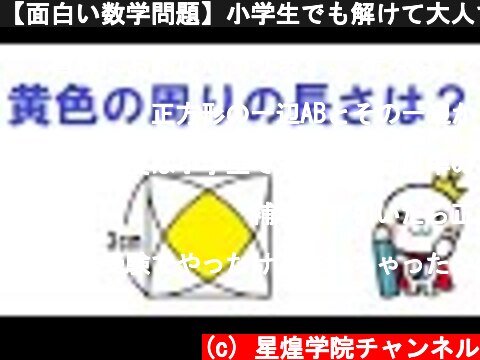
正方形の一辺ABとその一辺から円弧同士の交点の内最も遠い点Pを見ると、△ABPは一辺の長さ3の正三角形。そうすると、60°+60°-90°で、黄色の図形の一辺を見込む円弧の角度は30°と分かる。

今度は小学生でもわかる円周率の求め方やって欲しいです。

補助線を引いたら正三角形ができますね。計算はπを使って、最後に3.14に変換してもいいですね。

中学受験でやったけど忘れちゃった。僕は補助線を引かず円周上のある点から円の半径の長さを使えば円周を6等分できるという性質で正方形の頂点から黄色い面積の頂点までをπ、また扇が3/2πなので黄色い部分の一辺は1/2π、よって2πと出しました。

見たことあるし、解いた覚えがある。補助線を引くんだろうと何となくわかったが、解き方はキレイサッパリ忘れてる。

この問題面積を求めようと半年粘った思い出があるなあ

1.57を計算せずにそのまま4倍して約分すれば3.14×2だけ残るので、その方が計算ミス減るし楽なのでは？

これ、面積出そうとすると難易度上がるんだよなぁ中３の時に数学の先生に解説してもらってなんとか理解はできたが

正三角形の作図を知っていれば解けますね

知識2つの90°扇の交差で正三角形が出現する。

円弧同士が交わる点で、3分の1になっているから、6π×1/4×4/3でも同じ答になりそうです。

今回解けた！うれしい！

そうだ、積分しよう(脳死)

この問題の6cmバージョンでここの面積を求めなさいという問題を中学生の頃友達に出されたきり答えが出ても当たっているか分からないので教えて欲しいそうです。

求める長さは、円周の12分の4になるから、円周の三分の一で２π

小3の時、この図の面積を解かされましたね。

面積の出し方をおしえてください。積分でもいいので、、、

これ、やり方わかったし暗算でできて完璧やって思ってたんだけど2π……6.28……そっかぁ、π使わないのかぁって答えあってんのになんか悔しかった

頭が小学生で止まっているので解けました。

【面白い数学問題】簡単そうで難しい角度の問題

作図がうますぎて薄々答えがわかってしまうw

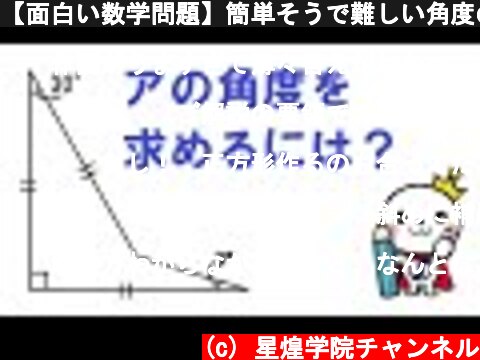
（ご解説の要領での図解が視覚的にも非常にすっきりしていていいな、と感じました。一方で自分は、この手の問題の落ちは正三角形等を如何にセッティングするか、ということかと考え、少しごちゃごちゃした感じですが、次のように直接的に正三角形を設定しました。）問題の図において、各点を上から反時計回りにA、B（直角部分）、C、D（内側の点）とし、ABと一辺とする正三角形のもう一つの点EをABに対して右側に設定する（△ABEは正三角形）。△ABDにつき頂角30°の二等辺三角形だから、∠ABD=75°、従って∠DBE=∠ABD-∠ABE=75°-60°=15°。△ADEも同様に頂角30°の二等辺三角形だから、∠DEB=15°。ここで△BDCにつき、∠DBC=90°-∠ABD=15°、BC=BEより、△BDEと合同になる。即ち、求める∠DCB=∠DEB=15°。

よし！　正方形作るのも合ってたし、回答も合ってた！スッキリしました👍

むむうー　斜めに補助線を引いたけど解けなかった！難しいなあ😙

解き方わからなかったけど、なんとなく15度くらいじゃない？と思ったら本当に15度だったw

残念ながら解けないと言われた２本の補助線ともう１本の補助線（角アと15°を両端角とする合同な三角形を作る）を組み合わせると底角が(45°－ア)の二等辺三角形ができ、15°＋ア＝45°－ア　∴ア＝15°

30°がポイントですね！(^^)

頭の中で解くには難しい

昇太師匠数学も出来るのか…

作図を見て、なんとなく１５⁰だと思った。正方形の左の辺を、左上を支点として３０⁰右に動かすと、左右の中央で止まるのだな。

直角二等辺三角形を作って、さらに15-75-90度の三角形に分解して、√2-√6 : √2+√6 : 4 の辺の比を使ってゴリゴリ計算しまくった私がアホでしたｗｗ

ありがとうございました。

上の30度と下のア繋いだ二等辺三角形にして180=90+ア＋30+ア＋30で2ア=30で15でいいんじゃ無いのコレ？

文章にするとわかりづらいですけど、同じ長さの斜めのやつの端っこから真横に補助線引いたら上が30°の直角三角形だから底辺が半分の長さってわかるから、そこからまた左下に補助線引いたら下の三角形が頂点が真ん中なので二等辺三角形ってことで90°-75°=15°って出したんですけど？

解けそうで解けない初等幾何はだいたい正三角形が絡んでいる気がします。自分は動画とは異なる補助線の引き方で解きました。30°の角からさらに反時計回りに30°回した補助線を引いて、左下の直角の点と結ぶと、左の縦の線と補助線とで正三角形が作れます。続いて、角アの伸びている先の点と、正三角形の右側の頂点と左下の直角の点とをそれぞれ結ぶと、2辺とその間の角が等しい合同な三角形（底角15°の二等辺三角形）が作れ、したがって角アが15度と分かります。

くそーまた、補助線で違ってた！補助線センスが欲しい😢

僕は補助線を直角のところの点から、一番角度が大きいところの点に引いて、上の部分に二等辺三角形を作り、二等辺三角形は底角が等しいので（180−30）÷2＝75°になって、したの三角形の左の方の角を90-75＝15°と求めることができ、補助線のしたの三角形も二等辺三角形だから、同様にして角アは15°と求めました

正方形かぁ〜

解答、分度器を使う。

もとの図形と合同な左右を反転させた図形を左側にくっつけてＦＦ７の黒魔道師ビビの帽子のような形を作ります。そして、凹んでる角の部分同士を線で結ぶと正三角形ができて右下に平行四辺形ができます。平行四辺形の対角＝頂角30度の二等辺三角形の底角－60度＝15度＝アでできました。

【面白い数学問題】きまりが分かった！・・・あれ？

(c) 星煌学院チャンネル　（オリジナル問題）小学生・中学生向け学習塾を名古屋市・知多市・東海市・安城市・大府市で展開する星煌学院の動画です。

2021については45^2-2^2の和と差の積にできるというのは受験前にかなり話題になっていましたね。

適当に素因数分解したら簡単に解けました😁

「43×47があります」で終わるのでなく、「こう考えて分解します」とか「地道に探していくしかないですね」とかの様に探し方にも触れた方が良いのでは？

西暦って模試でも問題に出てくるから、受験の年の西暦の素因数分解と対数取った時の桁数とか事前に色々おぼえてたわ

平方数を40~50まで暗記してるからとか話題になったからとかあって45^2-2^2は見てわかる

とんちをきかせたナゾナゾかと思ったら、ガチで難しい数学問題だった件

それぞれが素数の個数であることは、すぐにわかりました。2021は素数の積であろう、ということも予想できました。案の定その通りであって、回答も納得できます。しかしここで終わってしまうと、数学(算数)的にはあまりにもクイズ的で物知りのための問題にしかならず、クイズ的にはあまりにも数学(算数)的でおもしろみに欠けます。その原因は、実際に解こうとすると多くの時間を要することです。試験会場でこのような問題が出された場合、時間をかけずないためにはどのように解いていけば良いのでしょうか？大きな数を簡単に素因数分解する方法があったら教えてください。

東京オリンピックが唯一”奇数”の年に開催されたオリンピックになるってニュースで見て、”素数”じゃないんだなって思って調べたことあった。

なぜ3の倍数7の倍数ではないか判別できるのかも教えてくれると助かります

解説聞いてもわからなかった。この手の問題サクッと解ける人すごいと思う。

どっかの別の動画で2021が素数じゃ無い事聞いてて、細かい数字は忘れてたけど解けたわ。

素数関連って言うのまではなんとか分かったけれども…43、47に行き着く方法を教えて欲しかった。やっぱり知識として覚えておくしかないんだろうか。

えっと、あー、法則性は分かった。じゃあ2021は…え、これ法則わかっても面倒くさくね！？　ん？　でも2021のアレってどこかで聞いた覚えが……迫　真　数　学　部

理解できるけど解けと言われて「俺に」解ける問題ではなかった()

これはたまたま他の動画で素因数分解したことあったからできたけど、正直それがなかったら2025が45²とはパッとはわからんかな。

「43と47が果たして発見出来るかどうか」出来るわけあるか

2021はインド式計算に触れてほしい

たぶん受験シーズンの子にとっては、2021=43×47は暗記してるだろうからそれ前提の問題ですね

45^2=2025, 2025-2021=4, 4=x^2, x=±24とか9とか来たら全部これだから(45±2)^2例えば2016=42×482205=？

数が奇数で位の和も3の倍数にならない上に1の位が5でも無いので素数か約数が少ないということはすぐに分かったあとは電卓でしたw

【面白い数学問題】答えが２つ？算数オリンピックにチャレンジ！

こういう動画って素直におもしろいし数学に長けてない自分でも解説を聞くとなるほど！って納得できるんだけど、それと同時に高難度レベルの数学の問題になってくると学力とか知識よりもとんちとか頭の柔らかさが重要になってくるんだなと思った

Aさんの年賀状を受けとれるのがどの家になるか大変な争いになっていそう

模範解答みたいな、しっかり数とか図形の性質を使って解く必要のある場面もあれば、999通のほうみたく頭を柔らかくする必要があるときもあるのが、数学かなと思いました。

「Aの敷地が超巨大」という前提がOKなら「家がそれぞれ空中に浮かんでいる」と言う前提もOKなはずなので『3次元の接吻数(=12)-１』の11通も正解になりそう。

まず模範解答通り5通と出した後、家を3次元に配置するのはありうるなと思ったのですが、敷地の面積の概念は思いつかなかったです。なるほど…。

2個目の解答のAさんみたいな家に住んでる人は間違いなく大金持ち権力者大地主だから、市民はAさんに媚びないと生活できないため別に家が近くになくても全員年賀状出すって解答好き

求められている答えとは絶対違うだろうが、９９９枚しか思いつかないwそしてやっぱり求められていた答えとは違ってた。

2番目の中心にクソでかい家建ててその周りをちっちゃい家で囲むことしか思いつかなかった後半でちゃんと説明してくれて嬉しい

丘の上とか高低差があれば6は行けると思ったけど、別解はそっちじゃなかった

999しか思いつかなくて、2つ目の答えってどんな発想の逆転が求められるんだ…ギブアップ！と思って動画開いたら、ただ単に僕が数学できないだけだった…

サムネ見て2つ目先に思い浮かんで999しかないでしょwwwって思ったら模範解答が賢くてなんか恥ずかしくなった

最初正六角形の真ん中と頂点に配置したら6になるから5が正解だって思ったけど、アリの巣みたいな配置にしたらその限りじゃないな…みたいなこと考えてたらその遥か上を行く解答があってもうお手上げです

理想値(999)って答える→実はもっと貰えました〜wみたいな流れかと思って、1000以上にならないか必死に考えちゃったw

テストで出た時、答えの書き方としては「Aの家を点と考えた時〜」みたいな書き方をするのが正解なんですかね。

最初のやつなら家は全て合同でxy平面上に存在すると定義すべきだね

模範回答以外の2つめで、平面ではなく空間で捉えて家が地下や上空にあるパターンを想定しました笑

みんな5個は簡単に分かってるみたいですごいな……ある家を原点とする直交座標で、x,y軸上の正,負にそれぞれ家を配置して4個までしか思いつかなかった。

まだまだ別解はありますよね。何も距離は平面だけではなく、3階建てのアパートの2階に住むことも考えられる。つまり、立体的に考えることもできます。一番近いが、直線距離なのか、道のりなのか、移動時間なのか、そういうことも考えられますね。

最初直感で999枚じゃないかと思ってて、冷静に考えると5枚かなと思ったんだけど、直感をもっと信じるべきだった。家を点とみなすのはサボりでしかないので、どっちが正しいかと言われれば999枚かな。

さらにAさんの家の塀がx軸上にあり、他の999軒の家の座標が(2^n,2^n/2^1000)(n=1,2,…,999)なら999軒ともAさんの家が最も近くて家どうしの距離が全て異なるという条件も満たしますね

【面白い数学問題】小町算～答えを１００にするには？～

Excelで全通り計算したら、手計算じゃ絶対思い付かない解答出た1+234×5×6÷78+9(78で割る)1×2÷3+4×5÷6+7+89(通分が必要)1÷2÷3×456+7+8+9(456を掛ける)

全部足したら45になるのは知ってたから感覚的に8×9にしたら行けるかな？って思ったら行けちゃった

1+2+3+4+56+7+8+9+10=100を少し改造すれば、今問でも+記号だけで行けるかな？

回答はこれから考えるけど、こういう問題が出せるって、和算って凄いのですね。小町算恐るべし。

全部+だと45、17と72の差が55だから最後だけ×にすると100にはなるが他の解の有無とか難しすぎる

まず先入観として、括弧を使わない、つまり順番を変えてはいけないと思ったので括弧は使いませんでした。順番を変えてはいけないというのにとらわれすぎて、掛け算は先に計算することを忘れていました。その結果、回答が何も出ませんでした。動画冒頭をみた結果、記号を入れずにくっつけてもいいと知った瞬間に解答例2をすぐに思いつきました。しかし、全部に記号を付けて解きたいという気持ちがあったため、解答例1を見た瞬間、とても悔しかったです。

1×2×3×4＋5＋6＋7×8＋9=100と導きました。

1「0」2「−」3「＋」4「−」5「−」6「＋」7「−」8「＋」9と思ったが「0」は無しかぁ。

1+2+3+4+5+6+7+8×9=100しか思いつかない

1+［(2×3+4)+｛(5-6)×(7-8)｝］×9だいぶめんどくさくなってしまった

（1＋2＋3＋4＋5)×6−7＋8＋9でいけました

あてはめで二回目に出せました！

とりあえず1+2+3+4=10だけ作っといて、(5−6)×[7−(8+9)]で何とか強引にもう一個10作って掛け算するという形になってしまった…

1+23×4-5+6+7+8-9とりあえず適当に…。

来たと思ったら101になったもうやだ

1+2+3−4×5+6×7+8×9=100!

１+２×３×４×５÷６+７+８×９⇒１００　を思い付きました、がこれだと１+(２×３×４×５÷６)+７+(８×９)＝１００、という四則計算のルールにしないと１００になりませんでした電卓で順番に上記の数式を文字通りに入力すると４０５になります算数って不思議ですよね（ちなみに動画の説明を聞かずに考えてしまったので、小町算の特殊ルールである隣り合う数字をくっつけても良い条件は考えずに捻りだしてしまいましたｗ）

142-3-4-5-6-7-8-9で出来た。邪道？