【面白い数学問題】黄色の部分の合計の面積は?

(c) 星煌学院チャンネル 小学生・中学生向け学習塾を名古屋市・知多市・東海市・安城市・大府市で展開する星煌学院の動画です。 HP: https://www.sj-seico.co.jp/ …
50過ぎたオヤジですが、勉強になりました。有り難うございました🙇
先生の優しい表情、丁寧な言葉使い、解説も分かり安いです!(59才、男、小学生に戻って勉強する気になりました!)
この問題はほかにも色々な変形のパターンがありそうですね。自分は動画でのやり方と逆に、真ん中の台形を2つに切って左右の白抜きの部分に振り分け、正方形の半分の面積の三角形が2枚だから、という形で解きました。
面白い問題ですね!等積変形を駆使してますね
これは真ん中の黄色の部分を上下二つに分けて左右に振り分けて半分+半分で、正方形一つ分としても同じ事です。色々な解き方を説明しないと、先生の解き方以外は間違いだと勘違いする生徒がいるので、解き方はいくつも有ります。と説明した方がよろしいかと⁉️
以前コメントさせて頂いた者です。今回も面白かったです。ぱっと見、□1枚分なんじゃない?と思いましたが、数学においては「ぱっと見」は無意味ですね…笑
一昨年の特別区一類でも出題されていましたね。
見た瞬間に100だとわかった👍
これは目からウロコ
【面白い数学問題】正六角形の面積を求めよう!
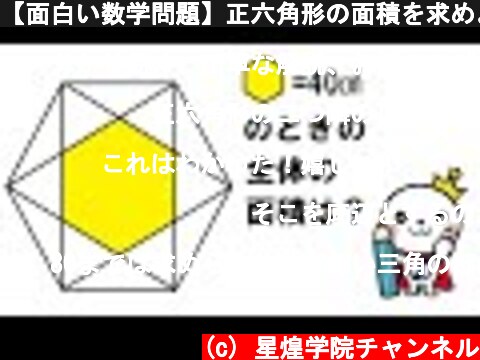
(c) 星煌学院チャンネル 小学生・中学生向け学習塾を名古屋市・知多市・東海市・安城市・大府市で展開する星煌学院の動画です。 HP: https://www.sj-seico.co.jp/ …
分かり易く、丁寧な解説、お話のスピードもゆっくりと、非常に好感のもてるビデオですねー!
正六角形の二つ隣の頂点同士を結ぶ対角線によって作られる六芒星は、元の正六角形の3分の2、その中心の正六角形は元の正六角形の3分の1という証明にもなりますね。
これはわかった!嬉しい!
そこを底辺とするのか!って思いました。これは一本取られましたね。
80までは求められたけど細い三角の部分ができなかった
辺の長さの比を出せば一瞬ですねひらめきさえあれば中学生でも暗算で解けるかも?
なぜ黄色は正六角形なんですか?なぜ白い小さな三角形は正三角形なんですか?
【面白い数学問題】もとの分数はいくつ?

(c) 星煌学院チャンネル 小学生・中学生向け学習塾を名古屋市・知多市・東海市・安城市・大府市で展開する星煌学院の動画です。 HP: https://www.sj-seico.co.jp/ …
初めて見る問題でした。いつも面白い問題をありがとうございます。私は、元の分母の差が15-8=7で、約分後の分母の差が4-3=1なので、7÷1=7倍すれば約分前の分数がわかると教えるところでした。動画を見て視点が広がりました。
俺の解き方⬜︎に整数を入れた時⬜︎+8が3の倍数、⬜︎+15が4の倍数になるものを探せばゴリ押しで解ける
3X=Y+34X=Y+15の連立方程式かな?
中学生の解き方 4×○=□+15-)3×○=□+ 8 ○= 7
【面白い数学問題】0 9999…=1って本当?

(c) 星煌学院チャンネル 小学生・中学生向け学習塾を名古屋市・知多市・東海市・安城市・大府市で展開する星煌学院の動画です。 HP: https://www.sj-seico.co.jp/ …
循環小数を分数にする他の方法でもx=0.999… 10x=9.999…9x=9 x=1になりますね。今まで気づきませんでした。
見た目は本当!ミリメートル単位の差しなら殆ど1に見える😀笑❗️
この計算を、電卓を使いますと、メーカーによって2種類の答えがあります。電卓を購入する時や、友達と比べ会いしておりました。
自分は普通の公立の小学校でしたがある時これに気が付いて、先生に質問したけど納得いかなくて質問続けたら怒られました(笑)
1/3 > 0.333333….ではないだろうか?と考えてしまうが自分の理解不足だろうか?
手品みたいで面白い!
( ^ω^)・・・なるほどw
えなんかで3分の1は3倍したら1になる数つまり0.3333…では無いって聞いたんだけど違うの?実際0.3333…って3倍したら0.999…だから0.333…と3分の1って=で結べない気がする
【面白い数学問題】ぜひ電卓を準備してチャレンジしてください。

(c) 星煌学院チャンネル 2~5の倍数の判別法:https://youtu.be/QsCOQE2kuHM 6,8,9の倍数の判別法:https://youtu.be/tDpezD1L4hU 7の倍数の判別 …
めちゃくちゃ面白くて楽しい問題ですね!友達にも出題してみます
1桁の整数Aは1の倍数と9桁の整数〜は9の倍数の記述ぶっちゃけあっても無くても関係ない情報っていう
へえめっちゃ面白かった!!何が面白かったって、途中までみて「あ、これ絶対987654321になるやつやん!」ってオチわかったつもりになっていたらそうはならなかったことwwそうわならんやろって数字の並びが唯一の解になってて逆に数学の神秘を感じましたねw
小学生の知識だけで解ける、面白い問題!!問題を選ぶセンスがすごい!
暗算で何度か迷宮に入りながら解いてみましたポイントは3桁区切りと、CDやFGHの関係性ですね偶奇も大事です7の倍数判定は少しだけ楽をしました(654)×10−(ABC)×10+G≡0(mod7)であればよいので、Gが7のときABC≡3,Gが3のときABC≡4を探せばよいといえます
数学とかきらいだったけどこのチャンネルは見ててたのしい
そろばん塾で講師をしていますが、面白そうなのでチャレンジさせてもらいました30分弱かかってしまいました。最後の桁はなんでもいいので、2,6と4,8を絞り、8の倍数の3桁、3の倍数の3桁の条件で矛盾しないのを当てはめて7の倍数になるか、と少々強引な形になりましたが、動画を拝見させてもらいましたところやはり7がネックになっていたので少し安心しました。良い問題をありがとうございました。
良問ですね♪最後7で割り切れて良かったです。答えが1つなのは必然なのでしょうか?そもそも答えがなければ良問にならないし、答えが複数あるようなら単なる問題ですし、たまたまなのでしょうか?答えが1つになることを予め知っていて良問を作ったなら凄いです。
めっちゃ書いたし頭使った…DとHを2or6に絞れることから、BとFを4or8に絞りました。「和が3の倍数」には気づいてなかった…おかげで奇数が地獄でした。おもしろかった☆
俺のやり方より「非常に短い道のり」でした(笑)。こんな条件に当てはまる数が存在するんですね。しかも一つだけ。面白い問題でした。…が、死にそうになりました。どこから絞っても大変そうなので、FGHが8の倍数から絞り込んだら大変でした。一応出ましたけど。
正に数学のコナン













![岡田斗司夫 [切り抜き] 編集ちゃんねる(Youtube 動画 pick up)](https://imitoha.com/c/imgc/UCwfyW7i8kAFUj8_tSSDT_PA/-a-input.jpg)







コメント