星煌学院チャンネル（おすすめch紹介）

チャンネル紹介

2021.12.22

【面白い数学問題】これで問題が成立するの？します！

(c) 星煌学院チャンネル　（オリジナル問題）小学生・中学生向け学習塾を名古屋市・知多市・東海市・安城市・大府市で展開する星煌学院の動画です。

問題をちゃんと読んでなくてAさん「わかりません。」Bさん「わかりません。」Cさん「わかりません。」と新しくCさんを生み出してしまったから全然わからなかった()

こういう取っ掛かりがあると一気に解ける問題好き

どんどん絞り込んでいくと時間かかったけどちゃんと解けた！嬉しい！こうゆう数学めっちゃすき

15分ぐらい真剣に考えて、ちゃんと当てれたの嬉しすぎる。そして良問すぎる

これは赤帽子白帽子と同じ考え方だな。しかし、あっちほど複雑じゃないのにちゃんと絞り込めるのは凄い。

AがBを論理的思考の出来る持ち主で必ずこう考えたはずだという絶対的信頼のもと、Aは正解まで導いている、BにとってはこれはAからの最大級の賛辞

中受算数ってこんな感じだった気がする。独特で、小学生範囲のことだけで色んな問題解けるの面白い

これは一の位と十の位の数字を、それぞれ縦軸と横軸に取ると視覚的にもわかりやすいと思う

B「わかりません」A「わかりません」B「わかりました」だと21になるのも面白いね

これは、AとBがお互いに、知ってる数字を教えれば一瞬で解決する。つまり、どんな難問が立ちはだかっても、個人でそれぞれ考えるより、コミュニケーションがいかに大事かを教えてくれる良問（文系）

こういう問題でいちばんすごいのはAの思考速度

十の位と一の位で分類した表を書くと分かりやすいな

脳内で条件を絞っていって解けた時の快感は異常

答え見ずとも分かった時の快感たまらん！楽しい問題をありがとうございました！

一見不可能に見えてちゃんと考えると解き方が少しずつ見えてくる良問。面白かったです

「4人の囚人帽子の色」とかで調べれば、もっとシンプルな問題がでます。「相手がわからない」というのも立派な情報ですね

Aさんこんなに賢いなら問題出された時点でメタ読みで64って分かるに一票

A「分かりません。」B「分かりません。」A「分かりません。」B「分かりません。」A「分かりません。」B「分かりません。」正解は64です。A「分かりません。」B「分かりません。」

A「分かりません」B「分かりません」C「ちくわ大明神」A「分かりました」B「誰だ今の」

この動画を既に見ていたAさんBさん問題「九九の答えになる2k…」Aさん「分かりました」Bさん「分かりました」

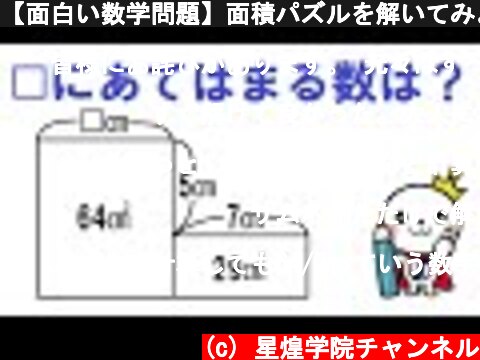
【面白い数学問題】面積パズルを解いてみよう！

(c) 星煌学院チャンネル　小学生・中学生向け学習塾を名古屋市・知多市・東海市・安城市・大府市で展開する星煌学院の動画です。 HP: https://www.sj-seico.co.jp/ …

皆様にお詫びがあります。元々はすべてのコメントに返信をしようと思い、時間を見つけて返信をしていました。しかし、予想以上に多くの方からコメントをいただき、コメントに返信をすることが難しくなってしまいました。コメントの返信は今後少なくなってしまいますが、できる限りコメントには目を通していきたいと思います。今後もコメントいただければ幸いです。

すぐ解けて良かった。大人になると数式とかもう覚えてないし、発想力で解けるパズル最高です。

ちょっとした発想でほとんど計算せずに求まるの気持ちいいなぁ

サムネ見ただけで解けるとなんだか嬉しい

ふつうに計算しても64/7っていう数字が出てくるあたり解答者に優しい問題ですねー綺麗な問題だといろんな方面から問題見れて楽しい

解けた時にスッキリ感を味わえる絶妙な問題を作るスキルは凄いなぁと思うきっとうまく作れた時はドヤ顔してんだろな

面倒な計算しなくても解けるとか面白いなー

2問とも1分くらいで解けた！こういう難易度の問題作るのすごいなぁ

結局、空きのスペースの面積に注目するところが、たいへん面白かったです。ちょっとした感動です‼️

解き方は違うけど初めて自分で解けて嬉しかった

数字のなれの差なんでしょうけど、2問目は普通に縦の長さ出したほうが早いやってなっちゃいましたね😂14は5で割れるやん！2.8やん！

先に分かったからめちゃくちゃ嬉しい

気持ち良い！もっと解きたい！

スッキリ解けた、滅茶苦茶嬉しい

29㎠の四角形で、縦をxと置くと、x✖︎7＝29より、縦は29/7cm64㎠の図形の縦は5＋29/7なので64/7cm横をyと置くと64/7✖︎y＝64なので　答えでもあるy＝7 と言うふうに考えました。

これは結構スムーズに解けた。うん、普通の思考で解けるぞ。

計算したら7に近い小数だったから、切り捨てた分の誤差で答えは7cmなのかと思ったら…なるほど！となりましたw

分数使う方が早いってコメも見られるけど、これら問題は分数を使わない「整数だけで解ける美しさ」だと思うんだけどなぁパズル要素と分かりやすい数字だから、小さい子に算数を学んでもらうには良問な気がする

こーゆー問題面積迷路でめっちゃやってたなぁ笑

縦の長さ(35+29)/7=64/7になって、分子ぴったり64じゃん！って気持ちよくなってホクホクしてたせいで、右上の空きスペースに目がいかなかった

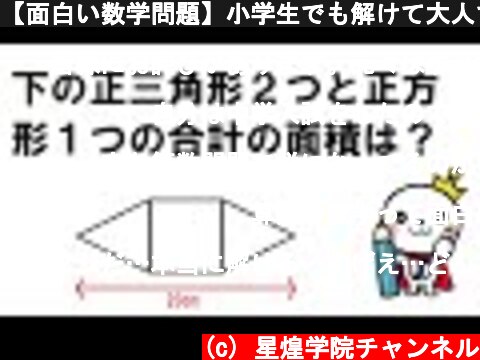
【面白い数学問題】小学生でも解けて大人でも解けない図形問題３

(c) 星煌学院チャンネル　2021/3/4にサムネイルを修正しました。小学生・中学生向け学習塾を名古屋市・知多市・東海市・安城市・大府市で展開する星煌学院の …

自分は中学入試をしたのですが、最近部屋を整理していると当時の算数の問題が出てきて、図形のページを見ると今では到底思いつかない所に補助線がたくさん引いており、あの頃は賢かったなぁって感じました笑学校の先生も「知識が邪魔をするから図形問題は中一が1番鋭い」って言っていたのも思い出しました。

変な算数問題で悦になってるのがいるが、このチャンネルはまともで面白い。

算数や数学って面白いということに大人になってから気付く…

マジだ…本当に解ける…すげえ…どんな発想で作ったんだろうこれ…

逆に特別な発想もなくゴリ押しで解けてしまう方程式や定理って発明よな

ゴリ押しで解くことも出来るけど、発想力があればかなり時短になるいい問題

面白い問題ありがとうございました15分考えても図形の移動方法が思いつかなくて、結局方程式で解いてしまいました…その発想はなかったので、完敗です笑

図形移動で正方形になるのも感動したけど、ごり押しで解いて400-300だけ残ったのも感動した｡

小学生でも解けるやり方を思いつくのが難しい

入試とかで建設業の問題とか出してほしい

1辺の長さを置いてゴリ押しでもいいんだけど、これは面白い。こういう発想を持って生活したら楽しいだろうな。

社会人になって数学から離れてしまったけど、数学が好きだった頃を思い出しました。

大人にも良い動画ですね、おもしろです。

いやーこの解法思いついた人は凄いなぁ。思いつかなかった

正三角形の高さと一辺の長さの比は、√3：２：√3【一辺の長さ】　20㎝ｘ2/(√3+2+√3)＝10√3ー10㎝【正三角形の高さ】　20㎝ｘ√3/(√3+2+√3)＝15ー５√3㎝【正方形の面積】　(10√3ー10)²＝400ー200√3㎝²【2つの正三角形の面積】　２｛(10√3ー10)(15ー５√3)ｘ1/2｝＝200√3ー300㎝²【答え】　(400ー200√3)＋(200√3ー300)＝100㎝²

正方形の1辺をaと置いて1:2:√3とか方程式を使って解いたら答えは合ってたけど、この数字ってことはもっとシンプルな解法があるんだろうと思ったら思った以上にシンプルだった。なにかに負けた気がする…。

小学生で解ける問題ということですから、ルートを用いなくとも正解できることはわかるのですが、ルートを用いたほうが簡単(?)だと思いとりあえずてやってみましたら、思った通り見事にルートが全部消えて答えが100になりました。それにしてもただの一辺が10の正方形の面積を求める問題がここまで形を変えて出題されていることに驚きます。

阿保だと三角比ごり押しが一番いいやとなってしまいますな

ルートの証明に使われる図形になりますね！中学生ならよりかんたんかも

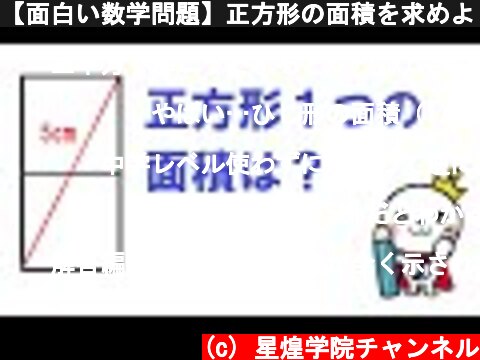
【面白い数学問題】正方形の面積を求めよう！

三平方で解こうとするとx²+(2x)²=5²5x²=5²x²=5ってなるのか

やばい…ひし形の面積（1/2対角線^2)を長方形に適用してしまってしまい、なんで答えが合わないか最初わからんかった…。

中学レベル使わずに解くって逆に難しい…

面積が5cmだとわかると対角線を底辺とした三角形の高さは2cm。同じ図形だと底辺がどんな長さでも底辺:高さ=5:2だから覚えておくと便利

解答編に至る思考の過程が全く示されていないのが残念です。この問題を初見した時に、一体どうやって考えれば「図形を拡張して考える」という「思考の飛躍」にたどり着くのかを説明して頂けますでしょうか？

三平方の定理知らなかったけど、これ、三平方の定理の証明方法なんやね三平方の定理をちゃんと理解できてるかどうかなんやね

小学校で全くおんなじ問題がでて、解けた時に先生が誉めてくれたのを思い出しました。これは解けると気持ちいいですね。

これは算数でやると楽しいやつ

三角形の面積が5だと勘違いしてたから一瞬で解けたわ

小学生の時栄光学園かどこかの過去問で似たような変形をする問題があった記憶があって、それで発想出来ました。高等な知識を要さずこういう柔軟なやり方で解くのはロマンがありますね

この動画は、呆け防止にいい。実にいい♪

三平方の定理の証明の一つで使う補助線の引き方してるわけだから、本質的には三平方の定理使ってるのと変わらないね

へえ。面白い。3×3マスに斜めの線を描けば、5cm×5cmの正方形の1/5って分かる感じか

三平方の定理が如何に便利な物かを痛感しますね。

拡大っていう発想なかった…すごい…

5x^2=25/4よりx=√5/2で、一辺は2xなので面積は5

直角三角形は3:4:5かと思ってた…

もとの図形のまま相似だけでもできるどの方法でも三平方の証明してるのと同じ

良い問題ですね。

直角三角形を3:4:5だと思っている人へ3:4:5になるのは、30度60度90度の三角であるものの場合ですなので正方形2段に対角線をひいたなら22.5度(正方形の対角線45度の半分)と67.5度の角が出てきて馴染みがないものになってしまうつまり正方形2段で描かれたものには正方形3段にしてみるのもいいのかもしれないてか三平方の定理つかわないって言ってたけど面積の問題かんがえてる時点で(それがたとえ論理的じゃなくて直感的なことだとしても)小学生からでも自然と三平方の定理に触れているんだと思う

【面白い数学問題】小学生向けの難問解けますか？

大人ですが、頭の体操にぴったりで面白いですね！先生の解説もとてもわかりやすくて、小中学生にもとてもよくわかると思います。先生の他の動画で問題に挑戦してみますね！

数列4つだけじゃ法則性決めつめるのにはちょっと足りないかもしれませんね。

中1「部分部数分解あたたたた」最近数列をやったので楽でした。これの一般式を求めるのが苦手だったのでたすかります。

今回みたいなパターンの数列の解き方高校の数学の先生に教えて貰って世界変わったの覚えてる

この問題をテスト時間内で解けるのか。。。すごいなあ💦

今となってはただの部分分数分解だけど小学生の頃は全くそんなこと知らなかったわけで学力ちゃんとついてんだなあ（語彙力）

声に出して言いたい数学用語「部分分数分解」

こういう特殊解って、問題見て見抜ける人ってスゴイよね。自分は、物理でも、問題ごとに数式が思い浮かんで解けるといったことが苦手だったんで、いつも同じ考え方で解ける解析力学を学んだとき感動した。天才でなくても、沢山の公式を覚えなくても、微分方程式さえ解ければ、あらゆる問題の式が自動的に出てくるからです。こういう天才肌の問題は性に合いませんね。

部分分数分解は数ⅡBで習うらしいんだけど全く記憶に無くて、数学系の動画で出てくる度に戸惑う

この系統の問題、中学受験の勉強で必ず出てくる

無限小数を足し合わせると有限小数になるとか美しい

6＋6＝12、＋8＝20、＋10＝30みたい感じで＋される数字が2づつ増えてるのかと思った

S=(3-2)/6+(4-3)/12+(5-4)/20+(6-5)/30+…=1/2-1/3+1/3-1/4+1/4-1/5+1/5-1/6+…=1/2. Ответ:1/2.

なるほど！最初は全く分かりませんでしたが。

これは屁理屈なのですが、n番目の項の分母が(n+1)(n+2)+(n-1)(n-2)(n-3)(n-4)*41.25や(n+1)(n+2)+(n-1)(n-2)(n-3)(n-4)(n-5)*8.25とすることで、1/9900が何番目の項か自由に設定できるので答えを90通り近く増やすことができますね。同時に上記の項の右項にn+m (mは任意の実数)などをかけてさらに変形すれば、無理やり任意の実数を答えに設定できそうです。

これ分母の1の数が98個で一番右と左の数をかけたのが200だから200分の98つまり100分の49になることを気づいた時は感動した

自分は分母が階差数列になってるから和を求めて分子は項数×１で出したけど、それを用いずに解ける人って言うのが本当に数学が出来る人なんだろうなぁ。

これ自力で思いつく小学生いたらすごいな。高校行ったら普通にやるので覚えさせるものではない気がします。

『頭の体操』を子供の頃やってたから、問題の式の分母が、＋6→＋8→＋10→＋12→＋14→・・・・・ってなってるかと思った。