数学を数楽に（おすすめch紹介）

チャンネル紹介

2021.11.09 2021.10.31

高校範囲の因数分解

(c) 数学を数楽に　オンラインプロ家庭教師始めました！！zoomを利用して直接川端が指導します。ホームページはこちら https://peraichi.com/landing_pages/view/r1c04 数学を解く楽しさ …

「x^8-16 を整数の範囲で因数分解」だと(x^4+4)(x^2+2)(x^2-2) でやめてしまう罠

複２次式の因数分解は、最高次の項と定数項で平方完成ですね

最近因数分解の苦手意識を無くそうとしてるので助かる

複２次式で定数項が平方数の因数分解は和と差の積に気づけるかどうかがポイントですよね。鈴木貫太郎先生から教わったことですが。

シンプルで難しい問題好き

お陰さまで出来ました。2乗ー2乗にもって行くしかないなぁと眺めていたら先生の解説通り解けました。

初めて解いたときは気持ちよかったｗ

複2次式は和と差の積を使うのは鉄則ですね！

前々から得意だったけれど受験で変なプレッシャーからかことごとく失敗してしまってから嫌いになっていた数学がこの問題解いてやっぱり数学が好きだと改めて感じることができました。ありがとうございます。

x^4+4k^4の形はソフィー・ジェルマンの恒等式ですね受験期よくお世話になりました

数検準2級の過去問でx^4+4が素数出ない事の証明が出てました。こうやって積の形にするんですね〜

2年ほど前に「インド式計算」の本を読んだ時、因数分解の応用だと知りました。数学がまた面白く成って図書館や書店で最近数学関係本をよく探す様に成りました。

これを知っておくと、後に習うことになる「相反式の因数分解」への応用ができる。

複二次式初見の時マジで訳分からんかったなぁ…

初見で答えまで行き着くことが出来たのですが、まだ因数分解出来るんじゃないかと頭を悩ませた挙げ句、動画観て「なんだよ笑」と思いましたw

一瞬　(x^2＋2)(x^2－2）だと思ったらプラスだった…

和と差の積って本当に便利だなぁ。

4次式はx²=tって置換すれば終わり(簡単なやつは)今回のはt²と4を使って二乗の()を作りに行く

中3のときにこの問題を問題集で見た時に、「新しい」と感じたので、当時色んな子に出しまくってました笑

これはまだ簡単な範囲かぁ

複雑にみえる連立方程式　慶應義塾

(c) 数学を数楽に　オンラインプロ家庭教師してます。 zoomを利用して直接川端が指導します。ホームページはこちら https://sites.google.com/view/kawabatateppei 数学を解く楽しさを伝え …

元の式を足すと100で割れて単純な式になる。逆に引くと２で割れて単純な式になる。それから求めるのが単純で良いのですが、受験だと整数ではない大きな分母に悩んでしまいますね。

x+y=ax-y=bからx=(a+b)/2y=(a-b)/2を導く方法は高校受験以降も何かと使うので経験しておくべき

力技好きな自分は無理矢理計算してましたね。和と差の積の実戦的な問題に使えたらより面白い。

個人的に、こういう問題って、解がきれいな整数じゃなかったらすっごい不安になる良い例です。

最初の解き方しか浮かばなかった(笑)。いろんな解き方考えられるのが頭が良いのだろうなぁと。

久しぶりに数学見たら面白い。というかスマートな解き方の追究楽しい。

対称性の良い式は足し引きすりゃいいってだけ

計算が少し面倒でした。100x+100y=3よりx+y=3/1002x-2y=-1よりx-y=-1/22x=-47/100x=-47/200,y=53/200

ad-bcが綺麗な値になったので逆行列の公式使って機械的に計算しましたw

(I)51x＋49y=1(II)49x＋51＝2この連立なら(I)＋(II)と(I)-(II)の式を作るすると100x＋100y=3 2x-2y=-1の２つの式が出てくるからこれを連立する方が良いかもそしたら2x-2y=-1は100x-100y=-50と表せて100x＋100y=3を連立すれば-200y=-53200x=-47となるからこれを整理してx=-200/47y=200/53個人的にはこのやり方かな

まさかのこの問題前のテストに出てきた、、、、テスト前に見たかった😭

この手の問題は、「足したら切りの良い数字になるから」じゃなくて、XYの係数が入れ替わっているから出来るので結構使いやすいですね

いやー二個目の解き方は美しいですね。そこには目が行きませんでした。途中で思わず成程！と独り言で言ってしまいました。いやーだから数学は面白い(=^▽^=)

2x+49x+49y＝12y+49x+49y＝2 x-y＝－2分の1

51x+49y=1を(49x+2x)+49y=1に、49x+51y=2を49x=2-51yに変形しても良さそう。この方法だとちょっと時間がかかるかな？

生徒が持ってきた学校のプリントにこの問題があったのを思い出しました(笑)　最初の解き方で解説しました。慶應義塾高校の問題だったのかぁ。

良いですねー！！(^^)面白い！

早稲田、慶應義塾系列の高校入試は難問もある一方、骨のある良問だらけなんだよなぁ😓特に慶應義塾志木は高校数学ＩAレベルの問題があるから勉強になりますね🤔

自分は連立方程式を足し算して100x+100y=3からx+y=3/100を導いて51x+49y=2x+49(x+y)=1に式変形し上記のx+y=3/100を代入して2x+49(3/100)=12x+147/100=12x=-47/100x=-47/200x+y=3/100に求めたx=-47/200を代入して-47/200+y=3/100y=3/100+47/200=53/200

対称性のいい2文字の二項間漸化式の解き方が題材なのかな

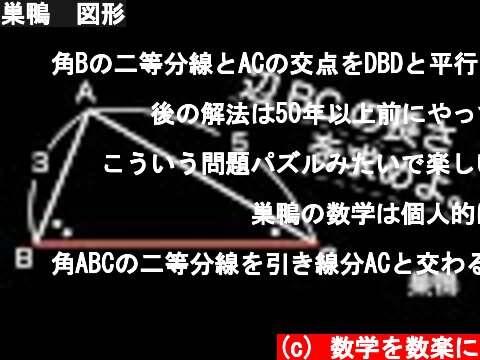
巣鴨　図形

角Bの二等分線とACの交点をDBDと平行でAを通る直線とBCの延長線との交点をEとして三角形BAE∽三角形AEC3:5＝5:BC+3というふうに解きました。

後の解法は50年以上前にやってたことを思い出して当時が懐かしかったです。

こういう問題パズルみたいで楽しいから社会人になっても解きたくなってしまうｗ

巣鴨の数学は個人的に大好き。解けた時の快感が半端ない問題がゴロゴロある。

角ABCの二等分線を引き線分ACと交わる点をDとして点Aから線分BDに垂線を引き、線分BCと交わる点をEとする。それでなんとかAD＝9/5,CD=16/5,BE=3になってメネラウス使ったらできた

相似と三平方の定理の二通りの解き方の説明は直ぐ理解出来ましたが、この問題の勝負所は補助線が引けかが全てだと思います。簡単なようで難易度は高いですね‼️

私は塾講師のアルバイトをしていてよく中学生に数学を教えているからか、見ていておもしろいなと思います

三平方による解法は面白いですね❤

ちゃんと同じ値になるところが凄いなぁ✨

数学ばっかり勉強してるからということもあり、流石に相似の形は直ぐに分かりました。

こういう教え方だったら、当時、図形問題嫌いにならなくて済んだかも知れない。

相似というアプローチで解くのであれば先生の仰る通り相似の式に元々の図形である△ABCが組み込まれた形が理想ですね。

受験は何十年前に終わったおっさんですいつもは動画を見てるだけで、それでもなんとなく解法がわかりつつあるようになりましたがやっぱり図形問題は実際にペンを動かさないとだめですね。今更ながらあらためて痛感いたしました。高校受験の数学はちょうど良いレベルなので川端先生の動画が一番楽しいです

当時の自分にリベンジできました。ありがとうございました。

貴方の動画ほとんど理解出来ました！！！私には貴方の説明が一番理解できる！！！有難うございます！今年で59歳になりますが40年前の理系時代が、懐かしく思えてきます！！当時、赤本や各学校出題参考書を良く解いていたな～ッ！！！

暗算無理です。角Ｂの二等分線とACの交点をＤとする。よってAB:BC=AD:DC=3:x (∵BC=x>0とした)からAD=5・(3／x+3)=15/x+3･･･①⊿ABC∽⊿ADBを定例句で認めればそれぞれの辺の比からAB:AC=AD:AB ∴3:5=15／x+3:3 (∵①)以上から ∴x=16/3

説明が本当に分かりやすい。

〇〇の意味が〇の2倍の角度を示すという事を綺麗さっぱり忘れ去っていた・・・

先生が大好きな、平方の差の公式を使うのかと思いましたｗ　8:30

中学受験算数ではAD=3x(3/5)=9/5 ,よってDC=16/5=BDで解きますね。

三平方の定理　計算できるかな？

数学嫌いな子をそういう方面から数学好きにさせる良問ですね()

解けたせいか値のせいか気持ちよくなった

急転直下の下ネタ好き

5:25 まずいですよ！

２つ目のやり方、x²＝53²－28²で解きました。xが整数にならなくてもともと、と思ったら整数になりました。最後に101倍しました。

こういう解説を聞くことで次からは101で割れることに気付けますね！ありがたい！！(^^)

101の倍数の答えを先に習ったから、101×9×5の時点で卑猥な数字が想像出来てしまった…

この先生が出す問題という時点でかなりの確率でどこかで和と差の積使うんだろうなってフィルターがかかる

カワバタ先生の変態ボイス聴きに来ました。やはり定期的に聴かないといけない身体になってしまったようです、、

一桁の数字が2つ並んだ数は11の倍数二桁の数字が2つ並んだ数は101の倍数三桁の数字が2つ並んだ数は1001の倍数四桁の数字が2つ並んだ数は10001の倍数五桁の……..ちょっと考えればそりゃそうね…

問題と先生を見た瞬間に和と差の積を使うとわかるから草生える

まず、ユークリッドの互除法で2辺の最大公約数を絞らないとね！！

1/101の相似な図形を用意したらやりやすいですね。

最初から2番目の方法で解きました。筆算での確認は53や28を上段に、101を下段に置くとビジュアル的にわかりやすいですね。

共通して101の倍数っていうのに気付けば楽ではあるけど、むしろ81、25の繰り返しから9^2、5^2で素因数分解出来てあと残った数字をちょろっとイジればokって考え方の方が賢い気がする。結果やってる事は同じなんだけどね。

これは昨日公開すべきだったのでは…(謎

数学や算数が苦手なので、寝る前に見てると瞬眠できます。

数学好きの方ならすぐにピンと来るのだろうが、当方全くもって101の事を知りませんでした。勉強になったというより面白かったです。

9×5が出てきた時に察してしまった…

和と差の積好きだね(笑)

負の数の商と余り

数学は「概念」が重要だと思い知った。

数学の勉強しすぎて、算数が出来なくなるパターン・・・

勘違いしている人が多いようですが、JavaやCとかの余りがマイナスになるのは絶対値最小剰余を使っているからではなく、0の方向への切り捨て除算をしているからです。これをやると0になる数が多くなりグラフィックとかの画像処理だとXY軸付近で歪みが発生してしまいます。絶対値最小剰余の場合は問題ありません。

プログラミング言語によって結果が変わる。余りが＋２(非負)になるか、-1(絶対値最小)になるかは言語次第なのでコーディング時に毎回どっちだっけ？てなる。EXCELは＋２になり、C言語だと-1になってしまうので検算するとき注意してるよ

昔引っ掛かって悩んだことがあり、懐かしかったです。余りのある割り算の概念で、整数を自然数で割る場合に限定されていましたが、こうした拡張の関係の解説をする場合にはこの制約はかなりきつい部類に入るように感じます。例えば730.29÷2.4=304…0.69や7/3÷2/3=3…1/3等は概念としてあまりのある割り算では成立していますが、今回の定義には当てはまりません。拡張概念の話をする場合には拡張の可能性をある程度広げておく必要があろうかと存じます。(商は整数)

ということは、7を3で割ると商2余1、-7を-3で割ると商3余2になりますか？なんか不便そうですね、絶対値ベースでルールを統一した方が技術計算、工学計算では使いやすそうです。

毎回胸ポケットに入れている各種ペンの透明の部分がキャップだと思ってしまう…

あまりが負の数になってはならないと言うことは知りませんでした。この数学の概念を習っていない世代です。小さな感動をありがとうございました‼️

中学の時、似たような問題で悩んでいたら、「数学的ではないと思うが、「余り」を釣銭と思えば、釣銭が負の数になるってのはそもそも支払いが足りてないんだ」と当時大学生だった兄貴に教わった。

mod を使う時は普通に考える事ですね

ふと、帯分数ってのを思い出した。マイナビの模擬試験に出てきてフリーズしてしまった笑

－3あまり2にしそうですが、ガウス記号と同じくこの定義が整数の除算の対称性（奇関数性）を崩しているんですよね。なので、個人的には手放しでは喜べない「定義」ですね。

余りが0以上である制約については初めて知りましたが、よく考えたら余ってるんだから負である訳が無いですよね勉強になりました

これは学校で教わった記憶がありませんでした。割られる数が正で割る数が負の場合　７÷（－３）＝商－２　余り１でよいのでしょうか。|b| ＞ｒ ≧ ０　という風に自分の中では整理してみたのですが・・・

[-7/3]=-3 のように、負の割り算でもガウス記号で囲うことで商を意味することに使えるわけですね

すごくためになりました。ありがとうございます。

電卓さんを使うと見事に当てはまらない