鈴木貫太郎（おすすめch紹介）

チャンネル紹介

2021.10.31

藤井聡太が小学生の時に解いた江戸時代の推理小説のような超難解詰将棋

(c) 鈴木貫太郎　過去動画の大学別・分野別検索はHPからhttps://kantaro1966.com この1冊で高校数学の基本の90%が身につく「中学の知識でオイラーの公式が …

この詰将棋は序盤に「犯人」が不可解な動きをします。その不可解な動きの謎が最後に驚愕な形で解き明かされます。

詰将棋シリーズ好きなので今後も続けてほしいですが、動画の締めとして最後に初手からツミまで一連で見せていただけると嬉しいです。

江戸時代に詰め将棋をパズルから芸術に進化させた。当時の日本人はすごかった

こういった詰将棋は一本道で読み潰していくというより、角を呼び込むのを気づけるかどうか、発想力も求められるので、芸術作品としては勿論、思考問題としても高い完成度なんですね江戸時代の作者も凄いし、本業じゃないのに一手一手の意味をここまで解説出来るのも凄い

将棋図巧第1番ですね将棋図巧は第98番「裸玉」、第99番「煙詰」、第100番「寿」が名作と言われてますね！将棋無双も動画で取り上げて欲しいです！

将棋ってほんと奥が深いなぁって思いました。。それと本当に将棋が好きなんだと感じました

図巧１番を変化を含めて丁寧に解説したのは初めて拝見しました。ありがとうございました。

改めて聡太君の凄さが分かりました、素晴らしい解説をありがとう❕🎵

解いた藤井二冠も凄まじいけど、考案した人も人間じゃない

手順をちゃんと元に戻していることに感心しました。数学だけでなく、このような動画も紹介してくださいませ。

超初心者ですが、詰将棋で難しいのは受け方を考えることです。受け方の逃げを間違えて「詰んだ」と錯覚して正解手順に辿り着けないことが良くあります。合い駒限定とか到底無理😭

この詰め将棋は１五飛に気付くかどうかですね😁この詰め将棋の白眉です😁

次元の違う打ち歩詰め回避が面白かったです。準備して解説しても大混乱で歩の数分からなくなる詰将棋を頭の中で解く小学生おそろしや。

はっしーは幻の「飛車不成」でしたね。

将棋界では広瀬九段が早稲田教育数学専攻で主席に近い成績を修めておられて、教授にも数学の才能を見込まれていたようですね。数学と将棋には最適解を求めるという共通点があると思います。

これはもう将棋チャンネル作るべきでは角ならず勉強になりました。

これは米長先生が詰ませた作品ですね。逆転のテクニックにありました。

奥が深いです‼️ありがとうございました‼️

渡辺2冠vs杉本8段でも角不成があったと思います！

コメントにもありますが、藤井二冠の師匠も角不成を決めてます。ちなみにハッシー云々言っていたのは飛不成で、これは流石に公式戦では未出現かと…。

ざ・見掛け倒し　複素数の基本

この1冊で高校数学の基本の90%が身につく「中学の知識でオイラーの公式がわかる」https://amzn.to/2t28U8Cオイラーの公式Tシャツ、合言葉は「貫太郎」です。https://www.ttrinity.jp/p/248613/

純粋に計算だけなら、x^2021^2021=x^5=1/x とした方が良さそうですね(追記)ついでにxの値を出さずに計算する方法与式=1/x+x=t とおく両辺から1を引き x(≠0) をかけて 1-x+x^2=(t-1)x左辺は0、x≠0 より　t=1

今回の見どころ5:55

おはようございます。久々に、貫太郎さんの “よっぱライブ” を聴きたくなってきました。全ての受験生に、 “明るい未来” を‼️

x^2021^2021= x^5が分かればx^3 = -1 , x^2 = x – 1を利用しても答えが出せますね。

因数分解を間違え、答えが-1になりました

虚数の定義が i^2=-1 だから,何とかしてiがi^2の形でしか出ないようにすれば,説明から虚数を排除できなくもないです。x^2-x+1 = 0 ⇒ (x-1)(x^2-x+1) = 0 ⇒ x^3 = -1 ⇒ x^6 = 1。　2021^2021 = 6n-1 (nは整数) だから、x^(2021^2021) + 1/x^(2021^2021) = x^(6n-1) + 1/x^(6n-1) = (x^6)^n/x + x/(x^6)^n = 1/x + x = 1。なお、1/x + x = 1 である理由は x^2 – x + 1 = 0 の両辺をxで割ると x – 1 + 1/x = 0 だから。x^3をセットにして説明してる間は虚数が出て来ませんが,x^2やx^1にバラした途端,虚数が出て来てしまいます。ところでその歌、この動画を見てる世代の人のほとんどは、知らないでしょうね。えらい古い曲が出て来たなあと思って調べたら、1979年の曲らしいです。八神純子さんと言えば、昔、私がヤマハの渋谷店(道玄坂)で買い物してて店員と話をしてたら、店員が「今△△さん(聞き取れず)が入って来ましたよ」と言われて、その人が店員の真横、私の1ｍ前に来て店員と数秒挨拶して奥に入って行ったのですが、挨拶のとき横からよく顔を見て初めて八神純子さんだと気づいたという出来事がありました。着てる物が上下ジーンズで,テレビで見るのと雰囲気が違うんだもん、わからないよ。昔、ラジオでコッキーポップ番組があってよく聞いてたけど、八神純子さんの曲も流れてた。八神純子さんはポプコン出身。

最初に答えを聞いて安心しました。あとは楽しみながら聞かせて頂きました。

遅くなりましたが、動画視聴ならびに答案のPDFアップを済ませました。https://note.com/pc3taro/n/n57984abd5f09xが1の原始6乗根（の1つ）である（2021^{2021} 乗しても (-1) 乗しても同じ値になる。）ことと、式の対称性から、xが1の原始6乗根のいずれであったとしても、式の値が1になることを確かめられます。

問題解説ラスト5分（笑）でも、このチャンネルのおかげで複素数平面や極形式が何ら怖くなくなった。ついでに、合同式や整数問題も怖くなくなった。元祖リモート授業だと最近思う。（笑）

問題を解くだけなら、複素数を持ち出すまでもないですね…。 ~~~~~~~~~~~ 　x^2 – x + 1 =0 …★　⇒　x^2 + 1 = x ≠ 0　⇒　x + 1/x = 1　…① また、　★⇒　(x + 1)(x^2 – x + 1)=0　⇒　x^3 + 1=0　⇒　x^3= -1　⇒　x^6=1　…② 一方mod 6において、　2021≡ -1　より　2021^2021 ≡ (-1)^2021 ≡ -1。よってある正整数pが存在して　-1< 2021^2021 = 6p-1（pは正整数）…③ と表せる。 ②, ③より　★⇒　x^(2021^2021) = x^(6p-1) = {(x^6)^p} * (1/x) = 1/x ゆえに①とから、求めるべき値は　(1/x) + x = 1。■

｜α｜＝1の時αの共役な複素数と1/αが等しくなるのは｜α｜^2＝α・αの共役な複素数から、｜α｜^2＝1α・αの共役な複素数＝1αの共役な複素数＝1/αでも証明できますね

x^2-x+1=0→x≠0としてよいのでx-1+1/x=0 ∴x+1/x=1(x+1/x)(x^(n-1)+1/(x^(n-1)))=x^n+1/(x^n)+x^(n-2)+1/(x^(n-2)) なのでan=x^n + 1/(x^n) とおくと，an-an-1+an-2=0となる。実際に求めると，a2=(x+1/x)^2-2=-1となるのでn=1から順に1,-1,-2,-1,1,2,1,-1-2,-1,1,2・・・となり6ごとに巡回している。2021^2021≡(-1)^5≡-1≡5(mod 6)なのでa2021^2021=a5=1 として求めました。

xは−1の三乗根であることはすぐにわかるから、六乗したら1であることはすぐにわかりますね。あとは、6でわった余りに気をつけてお終いかな。

これ、マークシートなら2秒で終わるなぁ。

おはようおざいます。私は複素数平面を高校で習ってない世代です。当初は°極形式を見ると、目が回っていましたが、おかげで最近は目がついて行くようになりました。ありがとうございます。明日もよろしくお願いします。

The question looks like a 💀 monster!

忙しい人向けのこの動画のスタート地点は14:16とはいえ、数学に限らず学問は基本的に「急がば回れ」だと私も思います。効率的にやろうとすればするほど大切な何かを失っていく気がする。

この手の問題の定石ですね。暗算は無理でしたけれど、合同式で進めると解けました。

指数のmod6でやったんご

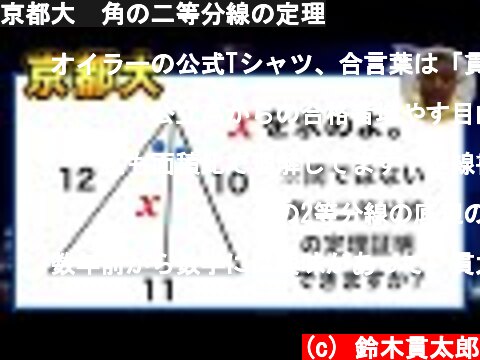
京都大　角の二等分線の定理

オイラーの公式Tシャツ、合言葉は「貫太郎」です。https://www.ttrinity.jp/p/248613/この1冊で高校数学の基本の90%が身につく「中学の知識でオイラーの公式がわかる」https://amzn.to/2t28U8C過去動画の大学別・分野別の検索はHPからhttps://kantaro1966.com

公立高からの合格者増やす目的で、こういう類の問題が近年出てますし、合格者も実際増えてますね。

私も面積比で理解してます　垂線書くだけで感覚的に理解でき、見通しがいいです三角関数を使えば、c:d=(1/2)axsinθ:(1/2)bxsinθ=a:b

角の2等分線の底辺の比より６：５．余弦定理　を通分してcosθを消去ｘ²＝90 x＝３√10私にもスッキリ出来ました。

数年前から数学には興味があって、貫太郎さんは基礎もやってくらはるから、本当にありがたい✨ありがとうございます😊💕✨

詩人兼農業技師の宮沢賢治の友人に当てた手紙には、ヘロンの公式が載っています。友人が病気になって肉体労働ができなくなったので,体を使わないような職業で適当なものはないかと宮沢賢治に相談を持ちかけていた時の話。「…差し当っては施肥量その他の問題で耕地の測量があります。耕地を簡単な三角形に分けて三辺を測り,それから面積を出すもので√三辺の和の半× (同一第1辺)× (同一第2辺 )×(同一第3辺)の計算など田一枚ずつですから一部落で何千と要るわけです。こんな仕事はいかがでしょうか」と。流石宮沢賢治さん。

4:37 夜中(2時)に見てたから死ぬほどビビった。こんな時間に玄関チャイムは怖すぎる…と思いきや鈴木家の家でした。

角の二等分線に対するベクトルは比が先に出るのでそれでやったら出ました。ただ計算は面倒です笑

倍角の公式を使うよりも、5^2=10^2+x^2-20xcosθにxcosθ=33/4を代入する方が楽で、計算ミスが少ないと思う。

角の二等分線の定理、今の私だと三角形の面積比からしか導けなさそうw

土日なんで久しぶりに貫太郎できました角の二等分線の定理の証明は平行線引くやつしかしらなかったです

おはようございます。貫太郎さんのおっしゃるとおり、”ヘロンの公式” は、正弦定理と余弦定理で証明できますね。実際に計算してみたことがあるのですが、sin, cos はすぐに消えてしまって因数分解の練習問題のような式になりました。見やすくするため三辺の長さの合計を “2S” とおくところが、工夫といえば工夫でしょうか？

そういえばヘロンの公式って名前でしたね。証明を習った記憶はないですが、高さ（垂線の長さ）をsinで表して、それを三角形の面積の公式をぶち込んだだけだなぁって認識してました。

6^2=12^2+x …の式を5倍、下の式を6倍しました～

4xcosθ=33 だったら24xcosθ=198 なので36=144+x^2-198 よってx^2=90

底辺を11-y,yとおいて余弦定理の流れで進めました。これだとyが整数になるということが明確にならず…二等分線なら初めから整数になってて進められます。これを知ってるか知らないかが分かれ目なのか。

(公式、三角関数、ベクトルの予備知識なしで)△ABCの角Aの2等分線とBCとの交点をPとし、AB上の点Qを角APQ=角ACPとなるように定め、△PQB∽△APB および △APQ∽△ACP からPB/AB = PQ/AP = CP/AC => PB=6 & PC=5AP*AP=AQ*AC=(AB-QB)*AC=AB*AC-(PB*(PB/AB))*AC=AB*AC-(PB*PC/AC)*AC=AB*AC-PB*PC=12*10-6*5

今日京大OP行ってきます！

ₐ△ͩ ̜ とし△⃝外接円とdの二等分線の交点をbとし、dbとacの交点をeとすると△dae∽△dbcで[da]:[de]=[db]:[dc]また方べきの定理→[de][eb]=[ae][ec]以上より[de]=√(12×10-6×5)ですね

交点からそれぞれ垂線下ろせば垂線は同じ長さなので、面積の比がそのまま底辺を分割することになります。　左右の三角形でそれぞれ余弦定理使ってｺｻｲﾝθを消せばxの方程式がすぐ出ます。その方が発想が簡単だと思いますがいかがでしょうか？

東大　大島さんと数学　球の体積

(c) 鈴木貫太郎　オンラインサロン→https://lounge.dmm.com/detail/3606/ 新刊「中学生の知識で数学脳を鍛える！８つのアプローチで論理的思考を養う』https://amzn.to/2UJxzwq ブルー …

貫太郎さんの独特のリズム感に合わせて喋れる大島さんすげー

高校数学の知識だけで説明してくれるのがありがたいです。体積積分についてのお話も聞いてみたいです。

高校の教科書には球の体積が円柱-円錐で求まると言うのが書いてあったので知ってました。しかし、錐の体積が柱の1/3というのは「義務教育で習ったから当たり前でしょ？」ってな感じのスタンスだったので改めて納得しました

大昔に読んだ数学者サージ・ラングの『さあ数学しよう!―ハイスクールでの対話』の中に、”πとは何かや、立体や球の体積はどう求めるか”が対話形式で語られていました。細かな内容は忘れましたが、読んで面白かったことはよく覚えています。

久しぶりの大島さん嬉しい!

寛太郎さんは映画レビュアーがお好きなのかな？今日の裏キーワードは「カバリエリ」でしたね。やっぱり立体図形の求積問題は高校までの数学の華ですね。次回は円柱の容器を45度傾けたら水はどれだけ残るか問題とか来たら嬉しいです。円柱なのに全然π出ないやつ。壊れるほど愛しても錐が柱の1/3のボリュームしか伝えられないのは、1997年にSIAM SHADE教授がるろ剣の定理として初めてお茶の間に示したんだと思ってましたmy heart.

なるほど〜、伏せた半球と、ひっくり返した円錐で、同じ高さの断面で両者を足すと底面の円になって一定、気がついた人、エライ！w

24〜25分頃の円柱のヤツは、「その”タマネギのスライス”は、どうせ後でh→0にするから、上面の円と下面の円が同じである『円柱』と見なしてよく、したがって、S(x)=πx²」とした方が解りやすいかなと思いました。いずれにせよ、積分を使っていいのなら、球の体積は「曲線y=√(r²-x²)とx軸で囲まれる部分をx軸を軸として1回転させたもの」と捉えて、機械的に積分計算したほうがスッキリしてる気がします。

この話は”真球のキャベツがもしあったら、その体積はどうなる？”って話を思い出しました。そのキャベツの体積は、一枚一枚の葉の面積の集合体…なので、∫0→葉の枚数dxで求められるという話（キャベツの芯はどーするというツッコミはなしでｗ）。微分と積分は逆演算の関係にあるのですが、これって機械的に覚えている人が殆どじゃないかと思います。”定義”を理解すればこういう面白い話ができる、ということで、ちょっと長いですが、30分飽きずに視聴できるかと。ブラボー。

これを中学生に教えるとき、「スライスしたときの断面積が常に等しいと体積も等しい」という考えを教えるのが一番難しいかも知れませんね。

おはようございます。貫太郎さんが、円錐の体積が円柱の体積の 1/3 になるのはなぜ？と別の先生に尋ねたとき「円錐の周り部分の面積が 2/3 だから…」との答が返ってきた、という話を聞いて、即座に「”トートロジー” じゃん。」と返した大島さんに、”真の知性” を見たように思います。

貫太郎は知識数学って感じで勉強にはなる

今日は長編解説動画だったので，今，視聴したところです。この説明を中学の時に受けたかったですね。

ほんとにおもしろい

ボリュームが凄い

後半の部分は、体積を微分すると、面積になる理由を理解してもらおうとしたから、若干難しかったのでしょう。個人的に思う話ですが、言語の理解は一定の考え方を共有しやすいですが、図形などの数学的思考は、言葉での表現が難しく、式とイメージが一体となって考えられないと、中々伝えるのが難しいと思います。

球の体積の証明法は積分利用1つとっても、いくつか考えられますね。大学流で言えば、極座標変換して3重積分で求める手がありますね。

面白かったです！✨検索したら江戸時代の関孝和も球の表面積と体積の公式を求めていたそうで、彼がどうやって公式を導いたのか知ってる人いましたら教えて下さい！

大学に4年もいて全く数学に触れていないと、円の面積の公式が怪しくなるって言うとんでもなく悲しい事実に気づいた。

多角錐の考えで1/3は良いとして、その考えが円錐にも適応できるかは流石にダメと思うのですが、その点は他の方法で証明できませんか？？

どっちがでかい？

64の13乗は2の78乗32の16乗は2の80乗だから両辺を2の78乗で割ると(63/64)の13乗　VS　(33/32)の16乗×4左辺<1右辺>4(終了)

7:30　急いでる人用7:17 「近似値で求めようと思ったらこうなったんで★てへっ★」鬼か！２の底の対数とったら78と80という数字がでたので「ほう…」とうねりました。実際電卓したら2.46×10^24、1.97×10^24とでたのでかなり差は出たので実際は鬼の僅差ではないのですが(24桁と揃ってる時点で十分鬼ですが)。意図も分かって解けたら気持ちいいすね！ありがとう先生！(夜勤明けで多少興奮しています)

ご紹介の、63と33の両方を変えて比較する方法が計算量が最も少ないですが、計算量が少し増えるものの、63のみを変える63^13/33^16 < 66^13/33^16 = (33*2)^13/33^(13+3) = 2^13/33^3 = (2^10/33^2)(2^3/33) = (1024/1089)(8/33) < 1 。とする方法もあります。

66^13を考えて、2^13<33^3より分かりました

最近の動画は試行錯誤の過程まで説明してもらえているのでとても勉強になります。ありがとう(=ﾟωﾟ)ﾉ

対数近似の問題かと思いきや、近しい数をみつけるというアプローチになるとは！わざとらしいなと感じはしましたが…対数近似作業を再確認するいい機会でした。

今日から仕事始めの方もいらっしゃるのでしょうね。コロナを取り巻く環境は厳しさを増すばかり。そんな中で外へ出て仕事をされる方におかれましては敬意しかありません。本日の問題。最初は2項展開？　では埒があきそうにない。3を底の対数も検討しましたが対数の値を評価するのが煩雑そう。ということで 63 は 2⁶ に近い数、33は 2⁵ に近い数ということに気付きlog₂ 63¹³ ＝13×log₂ 63 ＜ 13×6＝78　　∵ log₂ 63 ＜log₂ 64＝6log₂ 33¹⁶ ＝16×log₂ 33 ＞16×5＝80　　∵ log₂ 33 ＞log₂ 32＝5小さめに見積もったものと大きめに見積もったものを比べて小さめに見積もったものの方が大きいから、log₂ 33¹⁶ の方が大きいでしょ。すなわち 33¹⁶ の方が大きいでしょ。でした。実際、概算で出してみたら63¹³≒2.463×10²³33¹⁶≒19.780×10²³と思いの他、両者の差は大きいですね。本日も勉強になりました。ありがとうございました。

対数の話が続いたので，そういうやり方もあるのか？と思って見てましたが，やっぱりダメなんですね😄結局私も動画の最後の解法に落ち着きました。

対数の近似知らなかった勉強になります！

まさに翼くんのボールは友達になったつもりで、数字と如何に友達になれるかですよね。2や3というとサッカー⚽️でも良く出ますね。たしか、3-3-2-2フォーメーション？指数がついてるので、私も対数寄りでした。しかし、指数から対数に行く前に底に気づい底しまうと案外すんなりと行く問題でした。基本に忠実にというのは受験生だけでなく、社会人にとっても極めて重要だと感じました。脱線しますが対数の近似値を議論するとすれば、時間が許せばy=log3(X)のグラフを描き、微分積分(面積や接線)で評価するなど多角的な見方をすれば、数値の大小比較で悩む微妙な問題(東大2次？の3次関数の最大値最小値など絶妙)でも引き出しが沢山あると強みが出来ますね。ここに数学の素晴らしさがあるかなって思いますね。今朝も良問有難うございました。

問題自体はすぐに解けましたが対数の近似値の絞り込み方の話がとても参考になりました

酷いｗ対数を取りたくなるような数字を出してきて、実は…でも、よくよく考えてみると、”もっとわかりやすい数で比較する”というのも時間に追われる入試では有効なテクニックかも知れませんね。おそらく与式で騙された人が多数だろうから、これは貫太郎さんに拍手。

素因数分解してもどうもうまくいかないので、二項展開を考えたら(63+1)と(32+1)に気づいた。しかし、最終的な大小判定に二項展開すら必要なかったか・・

これはさすがにスケールが違い過ぎる…。本質的には「2数の比と1との大小を比べる」という単純な発想で解決（かなり雑な概算でOK）。 ~~~~~~~~~~~~~~~~ 63^13 < 33^16…①　⇔　(63/33)^13 < 33^3…②。ところが　(63/33)^13　<　2^13 = 8192　<　27000 = 30^3　<　33^3 だから、②は真であり①も真。■

おはようございます。双方を 33^13 で割って、”感覚的” には正解にたどり着きましたが、…。答案としては０点ですね。

入試でこれ出たらパニくるなあ

年末年始期間のため、遅くなりましたが、きょうは昼前に動画視聴ならびに答案のPDFアップとなりました。https://note.com/pc3taro/n/n00979690f05433も63も2のべき乗の数に近い（33は32に、63は64にそれぞれ近い）ということから処理いたしました。

僕が先ほどコメントで書いた、2つの「エレファントな解法」はパターン化できそうですn^m と k^lの大小を比較する場合 (n,m,k,lは自然数)n>kかつm>lだと答えが明らかなので、n>kかつm<lとするまず、n-k=jを計算して関数 f(x)=(x+j)^m / x^l を考える x=k付近で1より大きいか小さいかを議論すればよい f'(x)=(-1)×{(l-m)x+jl}×(x+j)^(m-1) / x^(l+1) l>mからl-m>0で (l-m)x+jlも(x+j)^(m-1) もx^(l+1)も x>0の範囲では必ず正の値をとるから、f'(x)はx>0で常に負になる(つまり狭義単調減少)f(k)が1より小さいことを言いたければ、f(k)<f(q)<1を言えるq(<k)の中で、計算が簡単になるものを探すf(k)が1より大きいことを言いたければ、f(k)>f(p)>1を言えるp(>k)の中で、計算が簡単になるものを探す(単調減少性の利用)このように関数を設定すれば、必ずx>0の範囲で単調減少になるというのが肝ですf(x)自体が適当に(正の)定数倍されていたとしても、最後の1より大きいか小さいかの部分以外では影響がありません

おはようござます。２の累乗に近いことまでは分ったのですが、そこから大小関係を導くところで頓挫。どうしても、等号の思考が頭から離れないですね、切り替えが必要。明日もよろしくお願いします。

そのアプローチの発想はなかっためちゃくちゃ勉強になった！！！

鈴木貫太郎に関する情報を厳選してまとめ！