ようつべ先生の数学教室（おすすめch紹介）

多変数関数のテイラー展開の考え方とその応用。[曲面論]

(c) ようつべ先生の数学教室　twitter http://twitter.com/ytsbess_main http://twitter.com/ytsbess_sub.

これは、テーラー展開の中でも、マクローリン展開ですか？

この辺になるともうギブアップですわ。高校数学あたりがちょうどいい

ねじりの公式の導出【材料力学】

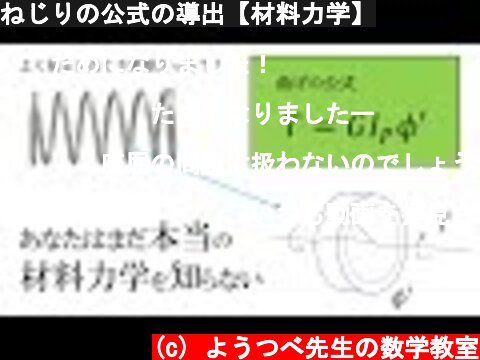
(c) ようつべ先生の数学教室　割愛シーン：連続体力学とのつながりについて https://youtu.be/7EW9wclcRow □ Twitter http://twitter.com/ytsbess_main □□ それではまた次回の動画で.

ためになりました！

ためになりましたー

座屈の問題は扱わないのでしょうか。ぜひ動画あげて欲しいです

いつも動画を拝見させていただいております。７月に大学院の推薦入試をうけるのですが、良ければ材料力学と熱力学の口頭試問対策の動画をだして頂けないでしょうか。

【2012九大】熱伝導方程式【伝熱工学院試対策演習】

(c) ようつべ先生の数学教室　

横浜国立大学 理工学府 の院試を解いて解説してくれませんか？

20分で分かるナヴィエストークス方程式[方向微分,ベクトル場]

(c) ようつべ先生の数学教室　集中力を奪う翁ありけり.

少し疑問に思ったのですが、vと∇の内積v・∇は、内積なので入れ替えて、v・∇=∇・vは成り立ちますか？

航空系学科b2の者です、大変わかりやすかったです。ありがとうございます

流体は無数の原子分子から成ると思いますが、動画内で説明されていた流体粒子というのはどのように定義されるものですか？

めっちゃわかりやすい！

多分、分かりやすい動画なんでしょうが、僕はなんとなく理解できたのかな・・・という感じでした。高校物理は得意なほうだったんですが（他の科目と比べるとですが）、流体は引き続き勉強が必要だと感じました。コメントで紹介されている「基本を学ぶ流体力学」が奇跡的に近くの図書館にあるようなので、さっそくようつべ先生さんの動画と合わせて勉強してみようと思います。今回もありがとうございました。

今回もわかりやすかったです！！1次元から2.3次元への拡張は1次元でいう位置を表すxが2.3次元へ拡張されてrになるので全微分を使うって解釈であってますかね、、

【2015九大】微分方程式の変数変換【数学院試対策演習】

(c) ようつべ先生の数学教室　

最後の答え (-lnx+A)x+Bx^2じゃないんでしょうか？(先頭のマイナスがない)

同じシャープペンシル