MathLABO〜東大発「みんなでつくる」数学ベスト良問集〜（マスラボ）（おすすめch紹介）

ゾッとする大小比較（愛媛大・医 2017）

(c) MathLABO〜東大発「みんなでつくる」数学ベスト良問集〜（マスラボ）　整数問題の全パターン解説はこちら https://youtu.be/thR1ZyXqDLE PASSLABOの数学特化チャンネル開講です！！ MathLABO〜東大 …

定番のe^πとπ^eの大小比較をしたことがあれば方針はすぐ思いつきますね。

logをとって、√3と√5の仲間にして。関数logx/x^xは、xは√3以上だし、x^xの方がlogxよりも増加量が大きいよなー、てことは減少していくよな〜…。と予想して方針立てしました。微分もすばるさんのお陰でバッチリ出来ました(^^)ありがとうございます

数値に差がありすぎてガバガバ不等式評価でも解けるの笑う

個人的には分数関数を作りたくなかったので、もう一回対数を取って√x・log(x)-2log(log(x))を評価しました

f(x)の範囲がx≧√3だと、f'(x)の範囲はx>√3 (端点が外れる)にならないのでしょうか？

一般性が無いけど、一番上に乗っている部分のルートの中身をそれぞれ4に置き換えたものを間に挟んで大小を考えれば暗算の範囲で出来るし、3と5でやっていることからして試験制作者の狙いはそっちな気も。

√4=2なので指数部はそれぞれ(√5)^√5>(√5)^2=5と(√3)^√3<(√3)^2=3(√3)^5=9√3>15.3よりも大きい数と、(√5)^3=5√5<11.5よりも小さい数を比べて終わり

地味に√3と√5ごとの分数を作るってとこ難しい

方針はすぐにわかったのですが、計算が難しかったです💦

必要な知識が数3なのか、数2Bなのかとか、どこでもいいから記載して欲しいな。

なるほどね。同じもの同士で揃えるのは発想なかった。とりま底を二乗して、揃えると3(√5^√5)と3((√3^√3 log[5]3))ここで指数の奴らで大小を見ればいい指数の方は明らかに左が大きい

logx(logx+1)って、logx × (logx+1)のように書かなくて大丈夫なのでしょうか？

複素数の問題やっていただきたいです

この程度の問題なら、√3^√5^√5 > √3^√5^2 > √3^5 = √243 > √125 = √5^3 > √5^√3^2 > √5^√3^√3 のほうが速いと思うが、それができるのは、√3^√5^√5=27.6917945…√5^√3^√3=8.034455…と値がガバガバだから。値がシビアだとなかなかそうもいかないので、動画の解法自体は押さえておいた方がよいかも。

√3^(√5^√5)>√3^(√5^2)=√243√5^(√3^√3)<√5^(√3^2)=√125だと何か不備があるのかな？

ベクトル全パターンだけ最後やって欲しいです😭😭

文系お断り問題の時はサムネに書いてほしい

京大実戦受けてきます！！(東工大志望ですが)数学の目標は5割ですかね、、

6:54 logの微分について詳しく知らないせいか、何をしたのか分かりませんでした。どういった処理をしてるんでしょうか？

eのおよその値は問題で与えられてるのかな？

あなたの数学力を試します。

(c) MathLABO〜東大発「みんなでつくる」数学ベスト良問集〜（マスラボ）　定期テストで出てもおかしくない良問ですが ３パターンで解けと言われたら難しい場合も？ 整数問題の全パターン解説はこちら …

【解法④】曲線y = x^2 / (x – 4) と、直線y=kの異なる共有点の個数が2個となり、かつ、共有点のx座標がいずれも整数となるようなkの最小値を考える。分数関数の微分と極限ができれば、この解法でも解けます。所謂、定数分離ですね。

y=x^2 と y=k(x-4) の交点を考えれば、直線が点(4,16)を通るとき k= -∞ となるがこれは交点が１つなので不適、よって点(3,9)を通る時が最小、ゆえに k=-9

√‬Dが整数であることは必要条件であり、十分でないので、（例えば解が3/2など）解を求めた後に必ず、逆の確かめが必要になると思いますが、どうでしょう？

なるほど！解法③は思いつきませんでした！何度か見返して完璧に使えるようにします！

α＝4は満たさないからα≠4って仮定してkを求めてもいいですか？

和がk、積が4kとなる相違なる2整数があるような整数kの最小値(言い換えただけ)kが自然数じゃなく整数ってのが、嫌らしいといえば嫌らしいね。とりあえずk^2-16k＞0は絶対なんですね。

(a≧b)一般性を失われないから言ってみたいね😅

別解f(x)=x^2-kx+4kとおく。2次方程式は高々2つしか解を持たないので、f(x)=0が整数ではない解を持つようなkは条件を満たさないことに注意する。k≦-10のときは、f(3)=9+k<0, f(4)=16>0 なのでf(x)=0は3<x<4に1つ以上解を持つので条件を満たさない。一方k=-9では、f(x)=0はx=-12,3と2つの整数解を持つため条件を満たす。以上より、求めるべきkの値は-9である。kをある程度小さくすると大きいほうの解が3より大きく4より小さくなる（もっと具体的には4に限りなく近づく）ことが実験的にわかり、記述もしやすいのでそれを記述してみました。

2つの整数解って整数の重解も含まれますか？

3つ目が思い浮かばなかった…

面白！楽しいよねん

解と係数との関係のときは必ず‪不等号はα≧βなんですか？

解法2みたいに考えようとしたけど判別式で進めてしまって二乗に気づけなかった…ちゃんと式から理解せんとダメだねやはり…

パラメタ分離が1番簡単かな?

解法3はなるほどと思いましたが、kが整数なら必ずしもふたつの整数解を持つとは限らないので出てきたkを代入して確認する必要があると思います

回答３間違ってないですか？

いや簡単～

2つの整数解を持つと言っているので、a、bともに0のときは考えなくてよいのでは？

最後相加相乗平均使いたくなる形

おはようございます！42日目！昨日見忘れた💦

【重要度★★★★★】最も差がつく“解の配置”を深堀りします。

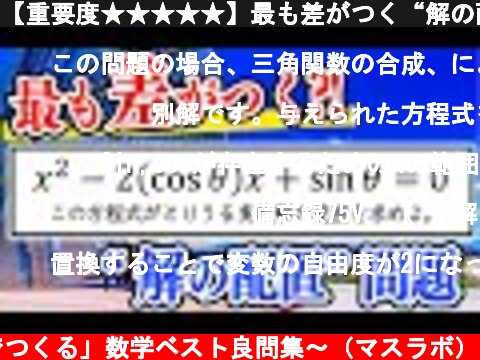
(c) MathLABO〜東大発「みんなでつくる」数学ベスト良問集〜（マスラボ）　変数としてxとθが混ざっている２次方程式 問題の意味を理解して、正しく翻訳する力と 視点を変えて条件を言い換える力が必要な問題でした …

この問題の場合、三角関数の合成、によりxの範囲を絞るのもかなり有力な手段、のようにも思いました。

別解です。与えられた方程式を変形すると、sin(θ+α)=-x²/√(1+4x²)、α=tan⁻¹(-1/2x)となる。この方程式があるxで実数解をもつための必要十分条件は、その式を満たすθが実数として存在することである。したがって、|sin(θ+α)|≦1となればこれを満たす実数θが存在するので、求める範囲は|-x²/√(1+4x²)|≦1である。以下、動画内の解説と同様実数として存在するための条件として、その文字を消去するという方法はよく出てきますね。この解法に慣れれば、軌跡や通過領域などの問題も簡単に見えてきますよ〜

Sin,cosが存在するためのxの範囲っていう解釈なんですね…面白い

備忘録75V” 〖 別解 〗【 式の中の一文字( 本問は x )の とりうる範囲の求め方 → 残りの文字が主役 】 ☆ 与式を満たす θ が存在するような 実数 x の範囲が求めるもの。･･･① ( よって、θ の方程式と解釈するのが 第1歩 ) 与式 ⇔ 1・sinθ －2x・cosθ ＝－x² α をある定数として 合成して、 √( 1＋4x² )・sin( θ＋α ) ＝ －x² ⇔ sin( θ＋α ) ＝ －x²／√( 1＋4x² ) これと ①を合わせて、 | －x²／√( 1＋4x² ) | ≦ 1 ⇔ x² ≦ √( 1＋4x² ) ⇔ x⁴ ≦ 1＋4x² ∴ x⁴ －4x² －1 ≦ 0 ( x²≧ 0 に注意して )⇔ 0 ≦ x² ≦ 2＋√5 ⇔ －√( 2＋√5 ) ≦ x ≦ √( 2＋√5 ) ■

置換することで変数の自由度が2になって、座標平面上の真理集合に帰着できるんだなぁって思った原像の存在条件に限らず、二変数関数は図示することで視覚化できるから良きかな

θの存在範囲でθを消すって意識があればめっちゃ簡単に解けます

θの関数と見て、sin(θ+α)かcos(θ+α)が−1~1の間に存在するためのxの条件でも行ける気がする

試行錯誤の挙げ句xを定数　θを変数　ととらえて三角関数の合成。与式の最大最小がx^2±√(1+4x^2)となります。この範囲に0が含まれるように不等式を解きました。

原像の存在条件をグラフでとらえるのすき

定数分離してy=-x^2/√（4x^2+1）のグラフ書いてyが０より大きい時交点持たないことを確認して、最後yに−1代入して四次方程式といて終わり。数3最強、脳死で解ける

三角関数の相互関係って奥が深いですな…

簡単に解けそうで色々詰まってる良問

x=cosθ±√(cos^2θ-sinθ)をθ∈R上で動かすのが直観的だけど、存在条件に帰着させて考えるのはだいぶお受験テクニックって感じ

sinとcos合成してθについての式にして不等式で挟んだら楽じゃないですか？

xの2次方程式が実数解を持つときのθの範囲かと思って、判別式で処理しちゃったわw

答案上、ｔ≧0を後から追加的に書く場合、時間が無くて、今回の様に□で囲って書くのは採点上は減点対象になります？

xがどうしても変数に見えてしまう呪いにかかっていると解けないやつですね…

二式を満たす（a,b）が存在するときグラフで考えていましたが、たとえ（a,b）が存在したとしてもその値によってはxが虚数解を持つこともあるのではないですか？私が何か勘違いしてるのかもしれませんが誰かお答えいただけると幸いです。

これがスーパー重要なのは共感

よくわかりました

偏差値68の校内実力模試で出題された問題｜整式の余りを２通りで。

(c) MathLABO〜東大発「みんなでつくる」数学ベスト良問集〜（マスラボ）　とある私立高校の実力模試で出題された問題です！ 単元をまたぐ良問ですね！しっかり完答できましたか？ 高２向けに出たみたいです …

解法1は、よく余りをさらに（x+1）＾2で割ったりするのを見かけるけど、微分が一番手っ取り早くて汎用性が高いと思いました！

今日も良い問題でした！特に、微分、二項定理を覚えた高校生は解けてほしいですね。自分は、最初解法２を思いつき、最後の２次式以下がまんま答えだな、というのは直ぐ分かり、解法１は余りを設定したところで手が止まり、動画視聴と同時に微分だということに気付きました！コメ欄の「通りすがりの数学者」さんが、余りをa(x+1)^2+b(x+1)+cと置く方が簡単とありますが、これは、素晴らしい着眼だと思います。細かいかもしれませんが、こういう細かいことを知っている、気付く、というのが数学は大事だと感じます。（現役のときに知りたかった・・・ｗ）

解法2で得られた式を微分してみるとわかりやすいと思います

二項定理って影薄いけど重いですよね…

備忘録70V”【 解法1 ~多重剰余定理 ( 微分法の応用 ) 】x³⁰＝ ( x＋1 )³・P(x) ＋ax²＋bx＋c ･･･① とおくことができる。両辺微分を繰り返して、30 x²⁹＝ ( x＋1 )²・Q(x) ＋2ax＋b ･･･②, 30･29 x²⁸＝ ( x＋1 )¹・R(x) ＋2a ･･･③ x＝－1 を代入して、1＝ a－b＋c ･･･①’, －30＝ －2a＋b ･･･②’, 30･29＝ 2a ･･･③’ 以上より、a＝ 435, b＝ 840, c＝ 406 よって、( 求める余り )＝ 435x²＋840x＋406 ■【 解法2 ~二項定理より、】x³⁰＝ { ( x＋1 ) －1 }³⁰ ＝ ( x＋1 )³・P(x) ＋30Ｃ28( x＋1 )² －30Ｃ29( x＋1 )¹ ＋30Ｃ30 ■

解法1で自分の答案と答え違ってまじか！って思ったけど、解法2で安心した笑二項定理は慣れるとかなり便利ですよね。多項式具体的に列挙できるので。（数学得意すぎる方の考えは分からないので、あくまで個人の感想です！）

恒等式は右と左が同じ関数だから微分しても同じ関数のはずx^2=x^2→2x=2xいろんなのに使う気がする

微分の考え方はテイラー展開の理論に用いられていますね。

ωv(3)＝1として、Xにωを代入する解答もありですかね？

解説中の計算ミスを「みんな気をつけて」に置換w

ミスすらも教訓にしていく男

計算ミスと見せかけて視聴者に教えたい事がある、さすがです。うちの娘に、東大生でもゴリ押し計算ではミスる事もある、と教えます。

後半の方法で解いたので、前半を見た時に｢しまった。計算ミスをした｣と思いましたが、後半を見て安心しました。

解法1は脳死で他に何も方針が浮かばない時に用いるべきで、計算ミスも誘発しやすくなる。この程度の問題なら解法2で解きたい。

今日も良問ありがとうございます！！

これいつも疑問に思っているのですが、微分しても等式は常に成り立つのでしょうか？定数が消えた分だけズレてしまって等式が成立しない気がします。

微分は一対一対応でやって、変形は、今日標問でやったんで出来ました！

微分が利用できる理由がよくわからないというコメントをいくつか見かけましたので、お役に立つかわかりませんが、この場をお借りして少し書かせていただきます。微分を使う方法は大本は以下の定理に基づいています。 「定理：整式f(x)がx=αを3重解としてもつ為の必要十分条件は、f(α)＝f‘(α)＝f‘‘(α)＝0が成り立つことである。」 ちなみに上記の定理の証明で用いた方法を帰納的に操作して、N重解バージョンに一般化することができます。2重解なら一回微分までの成立でOKです。必要であれば、上の定理の証明も紹介します。 さて、この定理を(x－α)^3で割ったときの余りを求めるのにどう使うのかというと、次のように考えます。 この問題は(x+1)^3で割ったときの余りを求めるので、以下の式が成り立ちます。 x^30＝(x+1)^3×Q(x)＋ax^2+bx+c(ここで、Q(X)は商、２次式部分は求める余り)ここで、f(x)＝x^30ーax^2ーbxーc とおくと、f(x)＝(x+1)^3×Q(x)となり、f(x)はx=-1を３重解としてもつと考えられます。この、f(x)に対して、上記の定理を適用するために、微分をすることになります。一応、これが正式な定理の利用方法なのですが、導関数の性質を考えると、余り部分を左辺に移項しなかったとしても、計算上は全く変わりありません。そこで、(ｘ-α)^ｎで割った余りを求めるときには、条件式を増やすために、とりあえず微分するという流れになっているというわけです。

二項定理の解法良いねぇ

問題　1以上3500以下の整数xのうち、x^3+3xが3500で割り切れるものの個数を求めよ。京都大学数学系の院試で数学Aの範囲で解ける問題です。難しい問題にチャレンジしてみたい人は挑戦してみてください。

ガウス記号、ひよってる奴いる？？

(c) MathLABO〜東大発「みんなでつくる」数学ベスト良問集〜（マスラボ）　ガウス記号にひよってる（アレルギーがある）方へ ２つのポイントさえ抑えれば難しくないんです！ (もっと言うと簡単な問題はグラフで考えると …

今年の一橋の入試に出ましたよね、、地方公立高校の自分はほっとんど習ってない分野なので、ガウス記号に限らず色々習わない分野の理解深めとこうと思いました

いつもガウス記号出てきたら終わったって思うから助かります。

備忘録70G” 【 (重要公式) 2x－1 < [ 2x ] ≦ 2x より、 】[ ガウスの解消が第1歩 ] 与式を代入して、 2x－1 < x² ≦ 2x これを解いて 0 ≦ x ≦ 2, かつ x ≠ 1 ･･･① この範囲で y＝ x² と y＝ [ 2x ] のグラフを描いて 見通しよく。 図より、x²＝ 0, 2, 3, 4 ⇔ x＝ 0, √2, √3, 2 ( ∵ ① ) ■

ガウス記号は数直線書いたらめちゃくちゃ簡単に定義式出てくるしガウス記号の定義は入試で絶対書いてあるから覚える必要すらない。ぜひ数直線で可視化してほしい。

ガウスみると拒否反応出ます。だいたいa≦x<a+1 を利用する形に持ち込むのが多いが……

y＝x^2とy＝[2x]のグラフを書いて図形的に解くっていうのも一つの方法だと思います。

おはようございます。このくらいの問題であればグラフを描いて確認してみるのが安全だと思います。今日もありがとうございました。あ、鈴木貫太郎先生の HP にガウス記号の問題がまとめられておりますよ。

最近、夏期講習でガウス記号の問題に触れましたグラフを書いて処理した方が方針が立てやすいって習いました

4:28の連立方程式の下の式にX＝±√kを代入したので、X≧0に気付かなかった。自分のやり方でやった場合これに気づく方法はありますか？

教科書に出てくるガウス記号の説明だといまいち理解できなかったので助かりました🙏

東工大オープンに出てきたガウス記号含む漸化式が全くわからなかった思い出…(もう3年前)

め↑っちゃ分かりやすい！

良い先生だな〜

7:40で、出てきた4つが答えだと動画で解説されていますが、この4つが答えかどうかは実際に値を代入して確かめる必要があると思います。なぜなら、「x^2=kかつk≤2x<k+1となるkが存在する」(これはx^2=2[x]と同値です) ⇒ 「x^2=kかつ0≤k≤4かつk≠1となるkが存在する」ですが、その逆が成り立つかどうかは分からないからです。もし、この問題がx^2=[3x]を解けというものだったら、k=[3x]と置いて同じようにやると0≤k≤9かつ(k≤1またはk≥7)となります。しかし、x=1は解になっていません。

グラフで共有点求めていけば瞬殺に見えた

ガウスアレルギーなので助かります🙏

MathLABOめっちゃおもろい

不等式のところ、[2x]≧kと書いてしまいそうなんですが、なにか対策はないでしょうか….

ガウス記号はその特性ゆえに極限で出されたら楽なんですよね笑

mが奇数の時、m⁵-mが240の倍数であることを証明せよ