MathLABO〜東大発「みんなでつくる」数学ベスト良問集〜（マスラボ）（おすすめch紹介）

存在する？しない？

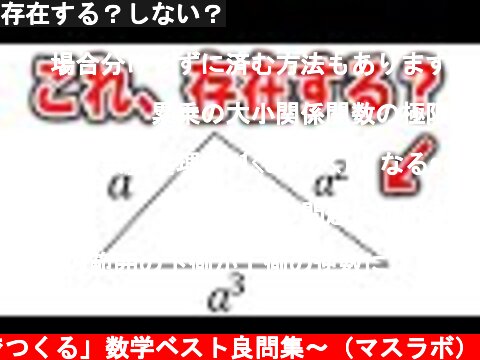
(c) MathLABO〜東大発「みんなでつくる」数学ベスト良問集〜（マスラボ）　三角形の存在条件、意外と忘れがち。 これ、ありますね〜。 整数問題の全パターン解説はこちら https://youtu.be/thR1ZyXqDLE …

場合分けせずに済む方法もあります。aの辺とa^3の辺は一方は最長,もう一方最短ですから2辺の差がa^2より小さければ作図可。つまり |a^3-a|<a^2 が存在条件。これを解くと|a^3-a|<a^2 ⇔|a^2-1|<a ⇔(a^2-1)^2<a^2 ⇔(a^2+1)^2<5a^2 ⇔ a^2+1<(√5)a ⇔ a^2-(√5)a<－1⇔ 4a^2-4(√5)a<－4 ⇔ (2a-√5)^2<1 ⇔ －1<2a-√5<1 ⇔ (－1+√5)/2<a<(1+√5)/2 。

累乗の大小関係関数の極限習ったらめっちゃ分かりやすくなった！

余弦定理で-1<cosθ<1となるaの範囲を求める考え方もあるよね4次不等式解くのはちょっとムズイけど引き出しは多い方がいいもんね

この問題に適用するには大袈裟ですが、Ravi変換して評価する方法もありますね。a^3+a^2-a>0, a^3-a^2+a>0, -a^3+a^2+a>0なる連立不等式を解くことに帰着します。

aの範囲の下側が上側の逆数になることが分かったので、計算量を減らせました。

辺をすべてaで割って、a²＜a+1であれば良いのではないかと考えましたa²－a－1＜0を解き答えとしましたが、なるほどaが1以下である場合はこの限りではないですね

答えに黄金比出てくるの良いですね

解けた問題でも、コメント欄見るとめっちゃ勉強になる。

|a^2-a| ＜a^3＜a^2+a から始めたら場合分けも不等式もそのままストレートに導けるのでは。

30年ほど昔に私が中学生だった頃に教わったヘロンの公式が初め思い浮かびましたが、公式を鵜呑みにすることはタブーで、三角形の成立条件から場合分けと二次方程式の解に行き着くことを思い出され、良い復習となりました。三次関数のグラフは高校数学Iの範囲ですが、それ以外は中学数学の問題のため高校入試で出題されてもおかしくないと感じます。

0<a<１→maxa　a=1 a>1→maxa^3に三角形の条件を入れればいいですね

aで場合分けすることまで思いつきましたが、三角形の成立条件が立式できずでした。勉強になりました。

マスラボさんの問題の中ではかなり易問ですねとはいえ重要な前提条件

三角不等式使わないのは意外だったこの問題の場合は難しくグラフを書くのではなくて、y=a^xを考えれば、a=1で場合分けするのは簡単に思い付くと思う

三角形の辺 a,b,cについて、a+b＞c (cが最大) の証明が知りたい！

A=1/aとおくと(ii)は(i)になりますね

余弦を利用してもスムーズにできるa^2 -(1+2cosA )a +1 = 0 まで計算して、aの係数を変数として判別式を解く。aの係数の最大(<3)・最小(=2)を求めて式に代入すれば答えが出る。まあ、その区間で関数が上昇することに言及しないといけませんけど

これはシンプルだけど盲点ですね。面白い問題

大体同じように考えたけど、0<a<1を忘れそうになった。

このサムネだと「a=1が存在する。以上」てなりそう

1分で素因数分解せよ（瞬間計算）

(c) MathLABO〜東大発「みんなでつくる」数学ベスト良問集〜（マスラボ）　昨日のドラゴン桜第７話で出題された 東大模試数学の類題を作ってみました！ 数学も「問題をつくる」側に回れば見る世界が変わります。

動画とは違う解法ですが書いておきます。70^2 < 5767 < 80^2 だから、5767 から 70^2 を引く5767 – 70^2 = 867867 = 12*70 +27（70で割る）なので5767 = 70^2 +12*70 +27 = (70+3)(70+9) = 73*79

「こういう問題って、平方根に近い素数同士の積なのがパターンだよな」って発想して、とりあえず初手73で割ってみたら割り切れた

一の位もしくは十の位を0にする(10で割って計算を楽にする)ために足していったら、ちょうど73足した際に73×80(=5767+73=5840)が出ましたので、80-1=79を因数に持つのかなーってなりました〜。ある数を足して、その後割り切れたなら、足した数で割り切ることは可能なので、結構早くできますね。オススメです！

もはや考えることをせずに素数を片っ端から割ってった(8分49秒)

70^2と80^2ではさみうちにして、75^2から調べていくのはいいですね。数学の内容とは逸れますが、時間のかからない探索方法として二分探索は大切ですので、そこに触れてもよかったかも。

4日目視聴！三日坊主脱却…笑理系のくせに数学アレルギーだけど、今日の授業はすごい楽しかったです。素因数分解したくなりました笑

昨日の問題のおかげで解けました！

パスラボで知った、インド式計算使って1分以内に解けた！(昨日のも出来ました)ありがとうございました！

質問です！！素因数分解した答えが例えば23×83(1909の素因数分解)のように、2つの数の差がかなり大きい場合、どのように解けば良いのでしょう？？

5767の末尾が7なので、一の位同士の掛け算の結果と考えると、1×7、3×9、7×1、9×3のいずれかしか無く、平均は、(1+7)/2=6、(3+9)/2=6、とどちらにしても中間値の末尾が6だということが解ります。今度は先頭を考え、7×7=49、8×8=64なので、86だと大きすぎて、76と推察する。5776=71・77は、77が11の倍数なので、11の倍数判定を既にやっているので、これではないことは確定。5776=73・7973も79も合成数ではないので、これに決定。

【自分用メモ】大きい数の素因数分解→2乗-2乗を探す！

下から17まで調べてダメだったから、19^3 > 5767なので素因数は2つ以下に確定 ならn^2 – m^2 = 5767となる適当なn,mを探すのかなという感じ

開平法を試したら余りが-9になったのでそれでいけました。

偏差値全然低いですけど、パスラボで前インド式計算見たのでその解法すぐ思いついてできました。

素因数分解問題に関する、解法のポイント解説に感謝します。　参考までに、私の携帯番号に5767が、含まれていました。　失礼ながら、貴殿の解説はとても明快です。2021.6.7　元数学教師の端くれより

75×75は、１の位が5で、10の位が同じ７です。教えていただいたやつだ！と勇んで、75の二乗をしました。すぐに5625とわかりました。（ありがとうございます！）でも、5767から引いてみたところ、142となってしまいました。平方数ではない・・・と、あきらめてしまいました。でも、解説がはじまってすぐに、あ！　次の76の二乗か！！とひらめきました。76の二乗も、インド式なら簡単に出せますね。通常なら、計算が億劫で、すぐに解説を読んだりして、あ～そ～か～自分にはやっぱりひらめきやセンスがないからな。なんてあきらめていたところでした。教えていただいた、10の位が大きいときの秘策インド式計算も復習しました。自分流に「潮出汁（うしろ足し）を前にかける」と覚えました。インド式で自分で出した76の二乗（5776）から問題の5767を引いたら、9になったときのうれしさは格別でした！いつもありがとうございます。まだまだ実力がありませんが、ついていきます！

いやあこれはおもろい！めっちゃ興奮した笑

5767が70と80の間なのは同じようにわかった5767の1の位は7なので因数の1の位はそれぞれ1と7か3と9になる10の位が共に7だとしたら、71✕77は違う、73✕79は5767→当たりこれで違ったらたぶん10の位を変えて61✕87とかやってたと思うまぁ、ある程度あたりをつけた勘になっちゃったねぇ

この問題はそれで早く解けるんだけど、比較的近い二つの素因数しか持たない前提の解き方なのがなー

70^2<5767<80^2なのは分かったけどそこからが思いつかなくてa×b(a≦b)の形にした時に下一桁が7になるのは(10n+1)×(10m+7)か(10n+3)×(10m+9)のどっちかしかないからゴリ押したwwwww記述だと0点になる自信しかないwwww

sin1,sin2,sin3,sin4 小さい順に並べよ【初見潰し】

(c) MathLABO〜東大発「みんなでつくる」数学ベスト良問集〜（マスラボ）　誰もが一度は引っかかる定義が大事な良問です。 僕も高２のとき、初見では意味わからず悩んだ覚えがあります。

-1≦sin(t)≦1で、-π/2≦t≦π/2の範囲で単調増加なので、この範囲で並べちゃえばいいよね。sin1=sin1sin2=sin(π-2)≒sin(1.14)sin3=sin(π-3)≒sin(0.14)sin4=sin(π-4)≒sin(-0.86)小さい順だと、sin4, sin3, sin1, sin2

なるほど、弧度法ってΠが入らずに、整数が入ることもあるのか。勉強になりました

備忘録55G” 〖 別解 〗【 弧度法の単位円を書いて、 π/2＝ 1.57･･, π＝ 3.14･･ に注意すると 】 y座標＝ sinθ だから、 sin4 ＜ sin3 ＜ sin1 ＜ sin2 ■

ﾊﾟｲを3.2として単位円を考えれば意外と簡単でした！

ちなsin1=0.84sin2=0.91sin3=0.14sin4=-0.76くらいみたいね…

3<π<4<2πより、sin4<0、sin1,sin2,sin3>0.次に、0<θ<πの範囲では、sinθはθ=π/2で最大となり、0<θ≦π/2で単調増加、π/2≦θ<πで単調減少する。また、sin(2・π/2-θ)=sinθよりsinθ(0<θ<π)はθ=π/2に関して対称である。以上より、f(θ)=|π/2 – θ|が小さければ小さいほどsinθは大きくなる.f(1)=|π/2-1|=|(π-2)/2|3.1<π<3.2より、1.1/2<f(1)<1.2/2f(2)=|π/2-2|=|(4-π)/2|3.1<π<3.2より、0.8/2<f(2)<0.9/2f(3)=|π/2-3|=|(6-π)/2|3.1<π<3.2より、2.8/2<π<2.9/2以上より、f(2)<f(3)<f(1)よってsin1<sin3<sin2∴sin4<sin1<sin3<sin2

一対一にありました。宇佐美さんの動画でやっと理解できましたありがとうございます

1ラジアンを度数法に直すとだいたい57度くらいなので最悪それを知ってたらゴリ押しできる

ラジアンは単位円上の扇形の弧の長さで中心角を表す物だというイメージが出来てれば慌てないですね

高校卒業して13年くらいになりますが、数学好きだったので、この問題はすぐに解けました(^^)

これは引っかかりますね

度数で考えちまった🤪で絶対違うと確信したのでラジアンで考えた！

おはようございます。単位円なり y=sinx のグラフなりでおおよその大きさを見たあと、あとは不等式による評価でオッケーかと（講義と同じですね）。今日もありがとうございました。

こっちの解説の方がわかりやすかったです。

フォーカスのステップアップに似たのあったな

もう暗記しています。Si2＞sin1＞sin3＞sin4

これはナイスなひっかけ問題！

ラジアンの定義から一辺1の正三角形とその一辺を半径とするおうぎ形を考えれば、1radが60度より少し小さいということがわかる。あとは単位円を使ってゴリ押し。

おはようございます。４/π ＜１＜π/３＜π/２＜２＜２π/３＜３π/４＜３＜π＜４であることが分れば、それぞれをsinでとってやり、プラスマイナス、単調増加・減少を考慮してやれば出てきますね。

これ度数表示と勘違いしてたわ弧度の表示か

衝撃の大学入試『嘘つきは誰？』

(c) MathLABO〜東大発「みんなでつくる」数学ベスト良問集〜（マスラボ）　2009年の千葉科学大学の入試問題です。 実は小学生でも解けますよね・・・？ （数学的な記述は少し困りました笑） 整数問題の全パターン …

マスラボはいつも面白い問題出すので毎日が楽しみです

三浦俊彦先生の「論理パラドクス―論証力を磨く99問」「論理サバイバル―議論力を鍛える108問」「心理パラドクス―錯覚から論理を学ぶ101問」は読みやすくて面白いのでおすすめです。 今回の動画のような論理問題がたくさんあって、その答えも書いてあって愛読書です。

この手の論理パズル、私には一番勉強になるから、週一くらいで出していただきたいが、受験対策としては問題ありまくりになっちゃうね…。すばるさんがLGBTQ…に配慮して発言しているところに時代を感じる。

おはようございます。できました〜。こういうの、受験算数でもありそうですね。解説のような考え方ができなければ、三人それぞれ正直者である場合と嘘つきである場合にわけて考えてもよろしいかと思います。今日もありがとうございました〜。=ↀωↀ=

答がわかりきった問題を厳密に記述することは数学では重要ですね

『嘘付き』を嘘にすると『正直者』なのはわかってましたけど、『3人嘘つき』を嘘にすると『2人嘘つき』でも良いのでは？とか思い始めて思考が止まってしまいました笑笑

The Hardest Logic Puzzle Ever というのがあるらしいなので、できたら解説お願いします。

一見して各条件が同時に成り立たない問題はそこまでの難度ではないですね。数学的証明という点で順を追ってしっかりできているかということを見るうえではいいかもしれないですね。

これ見て「まぁ場合分けだよね当然」って思える人は数学的な力も高いと思うよ

受験数学の問題としては、こういうのって少ないけど、昔の日大の医学部の問題になんか似たようなのあった気がします。かなり古いはずですが・・・国家試験まで手を広げていいのなら、公務員試験の科目の中に、判断推理っていう分野があって、そこだとかなり難解な論理パズルの問題が出てきます。

全員で3人という記述が問題文に欲しいです

こういうの待ってた

Aさんの記述を「3人とも嘘しか言わない」にすると、これ自体が成立しなくなるのが面白いといつも思う。数学的に表現する能力がないのが残念だが。

むかし、総当り戦で全員の勝ち数が異なる場合は、誰が誰に勝ったか分かるっていう問題あったけど、あれとはまた違うのかな☆彡

やっべ、数学の問題であることすっかり忘れて普通に記述のこと考えないで解いてた

『数学ガールゲーデルの不完全性定理」であったけど一般化して、これn人でやると「n-1人が嘘つきだ」って言ってる人が正直者なのも、簡単に分かるよね

「レイトン教授と不思議な街」ってゲームでこれの５人バージョンがあったな

正直に自分が嘘つきなことをカミングアウトしてるのかと思って無理やん()ってなった

とりあえず2^3=8通り全部見れば分かるだろ、と思って試してたら、n人の場合に一般化した問題が作れることに気がついた

記述を大事にするなら、Bさんが嘘つきのときの仮定でも矛盾することを書いた方がいいんじゃないでしょうか？確かに、そのときは明らかに矛盾するので自明ですが、減点されないためには念のために書いた方がいいのではないでしょうか。答えが一通りじゃないこともあるので、それを念のために記述しておく的な。

e＜3を証明せよ（数学科からの挑戦状）

(c) MathLABO〜東大発「みんなでつくる」数学ベスト良問集〜（マスラボ）　ネイピア数eは素数と同様、奥深い性質がたくさんあるので 定期的に数３範囲の動画も作っていければと思います！ 今回は証明とその誘導 …

【訂正】(2) 9:45 の部分でanを求めた後, n→∞でeを求めていますがすごく厳密に言うとΣが入る場合は「中身の極限値→全体もその値に収束する」という結果になるとは限りません。高校範囲で上記の方法だと困難になるため、視点を変える必要がありますね汗今回難しいと感じた方は、大学に入ってテイラー展開を習ったら好きになると思います。高校範囲で示す例として、視聴者さんからいただいたアイデアを一例として載せておきます。( 2 ) の解答：n >= 2 に対して( 1 + 1/n )^n = 2 + Σ_{ k = 2 }^{ n } C( n, k )/n^kここで C( n, k ) は二項係数C( n, k ) = n!/k!( n – k )!を表す。k!・C( n, k )/n^k = n( n – 1 )( n – 2 )…( n – k + 1 )/n^k < 1これよりC( n, k )/n^k < 1/k!( 1 + 1/n )^n < 2 + 1/2! + 1/3! + … + 1/n!　…①2 + 1/2! + 1/3! + … + 1/n! < e　…②を示す。x > 0 に対して1 < e^x上記の x を積分変数に変えて両辺 0 から x まで積分すると1 + x < e^x同様に 0 から x まで積分を繰り返すと帰納的に次の不等式が得られる。1 + x + x^2/2! + x^3/3! + … + x^n/n! < e^xx = 1 を代入して②が得られる。①・②より( 1 + 1/n )^n < 2 + 1/2! + 1/3! + … + 1/n! < en → ∞ とするとはさみうちの原理よりΣ_{ k = 0 }^{ ∞ } 1/k! = e

これは通学前の忙しいときにのんびり見る内容じゃないので、休み時間にチョココロネでも食べながら じっくり拝見したいと思います。

難問というよりは誘導から証明まで解法が美しい良問ですねさすがは旧帝大数学科……！

(1)は左辺を二項定理で変形してあげると帰納法を用いなくても示せますよね！

一般に lim_{n→∞}A(n,k)=a(k) for all k であっても lim_{n→∞}Σ_{k=1}^{n}A(n,k)=lim_{n→∞}Σ_{k=1}^{n}a(k) とは限らないので，9:42 からの推論は誤りです．それは例えば 1=lim_{n→∞}Σ_{k=1}^{n}(1/n)=Σ_{k=1}^{∞}0=0 とか1=Σ_{k=1}^{n}(2/(k*(k+1)))*((1/n)+(2/n)+…+(k/n))=Σ_{k=1}^{∞}(2/(k*(k+1)))*(0+0+…+0)=0 などと同じです．

近日e<2.75を示せといった動画を見ましたが、明らかにこちらの方がわかりやすかったです。

極限て慣れたらめちゃ楽しくなりそう

(1+1/x)^xの増減を示しxに十分大きい数字を代入してe<3を示す(脳筋)

備忘録‘’70V ⑴ n ≧ 3 のとき、数学的帰納法■ n! ＞ 2ⁿ⁻¹ ⇔ 1/n! ＜ 1/2ⁿ⁻¹ ･･･☆ ⑵ 【 (重要定理) lim An＝ ‪α‬, lim Bn＝ β が成り立つとき、 lim An･Bn＝ ‪α･‬β が成り立つ 】 e の定義 からの二項展開〖 難 〗 【別解】マクローリン展開が 明快！⑶ ☆を利用して、 無限等比級数■

これは良問の旅　千葉大学編でやりましたよね。とても良い復習になり、誘導なしで解けました。

よかった…（2）の最後の説明がかなり怪しい話になっていたので心配でした。コメント欄で有識者の方が訂正されていたのでナイスでした！

k=7まで階乗で計算すればe<2.72も示せます

2006年の早稲田大学の理工学部の数学の第1問題で似たような内容が出題されております。

もう一つ誤りがあります． 10:37 の不等号は極限値の大小なので ≦ までしか判りません．ここは 1+1+(1/2)+(1/3!) はそのままとし，n>=4 の範囲では (1) を用いて，35/12 で押さえるなどの工夫が必要ですね． なお，(2) については，．．． 入試らしく「e^x の微積分を既知とする」なら，帰納法により e=Σ_{k=0}^{n}1/k! + (1/n!)*∫_{0}^{1}(1-x)^{n}e^{x}dx なので n→∞ のとき |e-Σ_{k=0}^{n}1/k!|<=(1/n!)*∫_{0}^{1}1*e^{1}dx→0． 数学科らしく「単調有界数列の収束性を用いて e を構成する」なら A(n)=(1+(1/n))^n, B(n)=Σ_{k=0}^{n}1/k! とおくと (1) から B(n)<B(n+1)<3， 2 項定理から A(n)<A(n+1)，A(n)<=B(n) なので n→∞ のとき A(n)，B(n) は収束し，それぞれの極限値を e, f とおくと，e<=f． また，n>m のとき A(n)=Σ_{k=0}^{n}(1/k!)*(1-(1/n))*…*(1-((k-1)/n))>Σ_{k=0}^{m}(1/k!)*(1-(1/n))*…*(1-((k-1)/n)) なので n→∞ とすれば e>=B(m) となり，m→∞ とすれば e>=f．

これは典型問題。下から2.5～2.71で押さえる問題や上から2.75で押さえる問題なども見たことがあります。いずれにせよ、和が計算できる級数で置き換えるのは常套手段であり、ネイピア数の場合はこの無限等比級数が多いようです。

9:42　ここ中のｎ極限使って0にふっ飛ばすのってeの無限積表示と同じでふっ飛ばしちゃいけない類のものな気がするんだけど……

∑の展開のときになんで初項が1になるのかわかる方いますか？1/0になってしまうと思うのですが…

＞ ネイピア数の証明とてもIQ低くて面白い字面。

キレイな問題だね

無限操作を2回やってるからこれダメじゃね確か解析入門にεδ論法用いた厳密な証明あったはず